【答案】
分析:(1)利用ξ服从二项分布,或确定ξ的所有取值,求出相应的概率,可得分布列与数学期望;
(2)①记“动点Q恰好能到达N点”为事件A,记“投掷i次,动点Q恰好能到达N点”为事件B
i,i=2、3、4、5,显然B
2、B
3、B
4、B
5两两互斥,利用互斥事件的概率公式,即可求得结论;
②方法一,利用排列知识,分别求出投掷2、3、4、5次时的情况总数,即可求得结论;
方法二,利用从第四项起,每一项都等于其前三项和,可得结论.
解答:解:(1)依题意得ξ服从二项分布,即:ξ~B
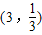
,所以Eξ=np=
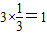
…(3分)
另解:依题意得ξ的所有取值为0、1、2、3
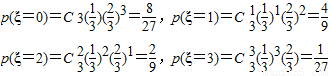
∴ξ的分布列为:
Eξ=
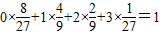
…(3分)
(2)①记“动点Q恰好能到达N点”为事件A,记“投掷i次,动点Q恰好能到达N点”为事件B
i,i=2、3、4、5,显然B
2、B
3、B
4、B
5两两互斥.
投掷2次时,分别投出2、3和3、2这两种情况,所以
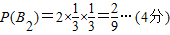
投掷3次时,分别投出1、1、3;1、3、1;3、1、1;2、2、1;2、1、2;1、2、2这6种情况,
所以
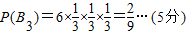
投掷4次时,分别投出1、1、1、2;1、1、2、1;1、2、1、1;2、1、1、1这4种情况,所以
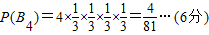
投掷5次时,只有投出1、1、1、1、1这一种情况,所以
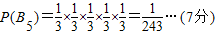
∴
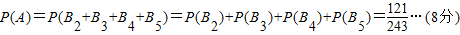
(2)②方法一:
投掷3次时,投出1个2、2个3、恰好能到达N点,此时不同移动方法种数有3种,…(9分)
投掷4次时,投出2个1、2个3或1个3、2个2、1个1或4个2恰好都能到达N点,此时不同移动方法种数有
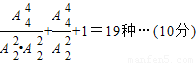
投掷5次时,投出1个3、1个2、3个1或3个2、2个1恰好能到达N点,此时不同移动方法种数有
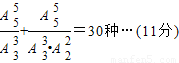
投掷6次时,投出1个3、5个1或2个2、4个1恰好能到达N点,此时不同移动方法种数有
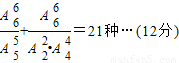
投掷7次时,投出1个2、6个1、恰好能到达N点,此时不同移动方法种数有
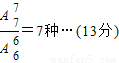
投掷8次时,投出8个1恰好能到达N点,此时不同移动方法种数有1种,
所以a
8=3+19+30+21+7+1=81…(14分)
②方法二:依题意得:a
1=1,a
2=2,a
3=4,a
4=7,a
5=13,a
6=24,a
7=44,a
8=81…(14分)
注:从第四项起,每一项都等于其前三项和.
点评:本题考查概率知识,考查分布列与数学期望,考查学生分析解决问题的能力,属于中档题.

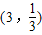 ,所以Eξ=np=
,所以Eξ=np=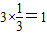 …(3分)
…(3分)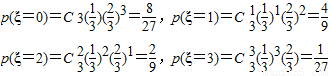
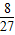


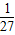
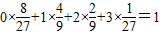 …(3分)
…(3分)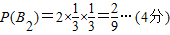
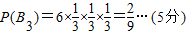
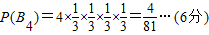
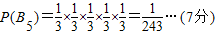 ∴
∴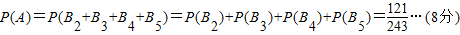
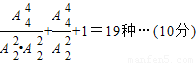
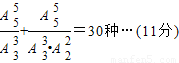
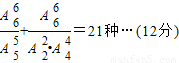
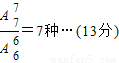


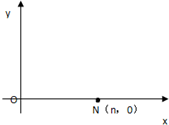 现有一个质地均匀的正方体玩具,它的六个面上分别写着1,1,2,2,3,3六个数字,
现有一个质地均匀的正方体玩具,它的六个面上分别写着1,1,2,2,3,3六个数字,