
已知z∈C ,z1 = ![]() ,z2 =
,z2 =![]() 。
。
⑴ 若![]() 都是实数,求复数
都是实数,求复数![]() ;
;
⑵ 在⑴的条件下,若复数![]() 在复平面上对应的点在第四象限,求实数
在复平面上对应的点在第四象限,求实数![]() 的取值范围.
的取值范围.
⑶ 若z1是虚数,z2是实数,且| z1 −z2|=![]() ,求
,求![]() .
.
解:⑴设z=a+bi(a,b∈R) ,则![]() ,
,
![]() , ………………2分
, ………………2分
∵![]() 和
和![]() 都是实数,
都是实数,
∴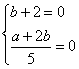 ,解得
,解得![]() …………………………………………4分
…………………………………………4分
∴![]() . …………………………………………………5分
. …………………………………………………5分
⑵由(1)知![]() ,
,
∴![]() , ………………6分
, ………………6分
∵![]() 在复平面上对应的点在第四象限,
在复平面上对应的点在第四象限,
∴ , …………………………………………………7分
, …………………………………………………7分
∴![]() , ………………………………………………9分
, ………………………………………………9分
∴![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]() . ………………………10分
. ………………………10分
⑶由⑴知,a+2b=0, z1 −z2 = −b+(b+2)i ……………………………………………11分
∵| z1 −z2|=![]() ,∴b2+(b+2)2=2得b = −1 …………………………………………13分
,∴b2+(b+2)2=2得b = −1 …………………………………………13分
z1 +z2 = −3b+(b+2)i = 3+i,∴| z1 +z2| = ![]() ………………………………………15分
………………………………………15分


科目:高中数学 来源: 题型:
. |
| z |
. |
| z1-zz |
查看答案和解析>>
科目:高中数学 来源: 题型:
. |
| z |
| z |
| 2+i |
| z1 |
| z2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| . |
| z |
| . |
| z1-zz |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| . |
| z |
| z |
| 2+i |
| z1 |
| z2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com