
已知 ,
, .
.
⑴ 求 的最小正周期;
的最小正周期;
⑵设 、
、 ,
, ,
, ,求
,求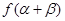 的值.
的值.
(1)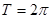 ;(2)
;(2)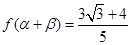 .
.
解析试题分析:本题只要考查三角函数的恒等变换、三角函数的周期、三角函数值求角等数学知识,考查熟练应用三角公式进行三角变换的能力、转化能力和计算能力.第一问,先将 中的括号展开,用倍角公式化简,再用两角和的正弦公式化简,最后将
中的括号展开,用倍角公式化简,再用两角和的正弦公式化简,最后将 化简成
化简成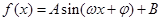 的形式,利用
的形式,利用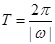 求函数的最小正周期;(2)先利用第一问中的
求函数的最小正周期;(2)先利用第一问中的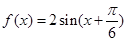 解出
解出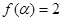 中的
中的 和
和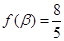 中的
中的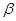 ,而
,而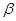 不是特殊角,则可以求出
不是特殊角,则可以求出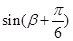 和
和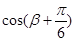 ,而所求的
,而所求的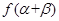 通过化简就是求
通过化简就是求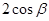 ,将
,将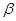 转化为
转化为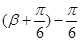 ,利用两角差的余弦公式展开计算.
,利用两角差的余弦公式展开计算.
试题解析:⑴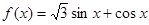 2分,
2分,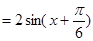 4分,
4分, 的最小正周期
的最小正周期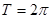 5分
5分
⑵因为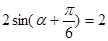 ,
,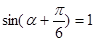 ,
,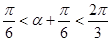 6分,
6分,
所以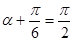 ,
,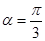 7分,
7分,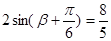 ,
,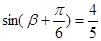 ,
,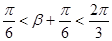 8分,
8分,
因为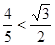 ,所以
,所以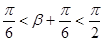 ,
,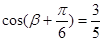 9分,
9分,
所以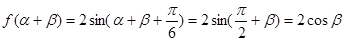 10分,
10分,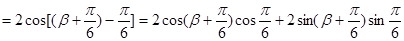 11分,
11分,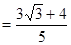 12分。
12分。
考点:1.倍角公式;2.诱导公式;3.两角和的正弦公式;4.两角差的余弦公式;5.利用三角函数值求角.


科目:高中数学 来源: 题型:解答题
设函数f (x)=cos(2x+ )+
)+ sin2x+2a
sin2x+2a
(1)求函数f (x)的单调递增区间
(2)当0≤x≤ 时,f (x)的最小值为0,求a的值.
时,f (x)的最小值为0,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数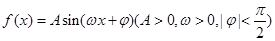 的部分图像如图所示.
的部分图像如图所示.
(1)求函数f(x)的解析式,并写出f(x)的单调减区间;
(2)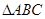 的内角分别是A,B,C.若f(A)=1,
的内角分别是A,B,C.若f(A)=1,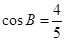 ,求sinC的值.
,求sinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 (
( )的最小正周期为
)的最小正周期为 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)将函数 的图象向左平移
的图象向左平移 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数 的图象;若
的图象;若 在
在 上至少含有10个零点,求b的最小值.
上至少含有10个零点,求b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=sin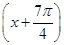 +cos
+cos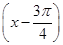 ,x∈R.
,x∈R.
(1)求f(x)的最小正周期和最小值;
(2)已知cos(β-α)=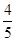 ,cos(β+α)=-
,cos(β+α)=-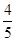 ,0<α<β≤
,0<α<β≤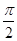 ,求证:[f(β)]2-2=0.
,求证:[f(β)]2-2=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com