

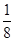 ��ʱ�������ͣ���������Ϊ38 882Ԫ��
��ʱ�������ͣ���������Ϊ38 882Ԫ��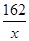 �ף�
�ף�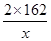 )��248��2x��80��162��1 296x��
)��248��2x��80��162��1 296x�� ��12 960
��12 960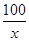 )��12 960
)��12 960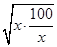 ��12 960��38 880(Ԫ)��
��12 960��38 880(Ԫ)��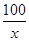 (x>0)����x��10ʱȡ�Ⱥţ�
(x>0)����x��10ʱȡ�Ⱥţ�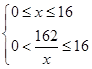 ����10
����10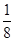 ��x��16��
��x��16��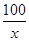 (10
(10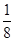 ��x��16)��
��x��16)��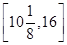 ������������
������������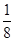 ʱ����ʱ
ʱ����ʱ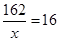 ����
����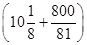 ��12 960��38 882Ԫ��
��12 960��38 882Ԫ��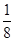 ��ʱ�������ͣ���������Ϊ38 882Ԫ��
��ʱ�������ͣ���������Ϊ38 882Ԫ��

 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
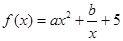
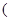 ����
����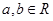 ������
������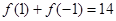 .
.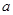 ��ֵ�����ͳ���
��ֵ�����ͳ���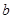 �IJ�ͬȡֵ���ۺ���
�IJ�ͬȡֵ���ۺ��� ��ż�ԣ�
��ż�ԣ� ������
������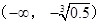 �ϵ����ݼ�����
�ϵ����ݼ�����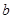 ����Сֵ��
����Сֵ��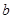 ȡ��Сֵʱ��֤����
ȡ��Сֵʱ��֤���� ǡ��һ�����
ǡ��һ�����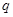 �Ҵ��ڵ���������������
�Ҵ��ڵ���������������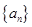 ��ʹ��
��ʹ��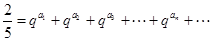 ����.
����.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ,����a������ij���.
,����a������ij���. +
+ +��+
+��+ �����.
�����. �鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ��������ͬ�㴦�������غϣ������������Ϊ����
��������ͬ�㴦�������غϣ������������Ϊ���� �ġ��Թ����ߡ������з��̣���
�ġ��Թ����ߡ������з��̣��� ����
����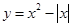 ����
����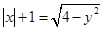 ����
���� ��Ӧ�������д��ڡ��Թ����ߡ����У� ��
��Ӧ�������д��ڡ��Թ����ߡ����У� ��| A���٢� | B���ڢ� | C���ڢ� | D���ۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
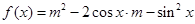 ��
��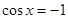 ʱȡ�����ֵ����
ʱȡ�����ֵ����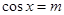 ʱȡ����Сֵ����ʵ��
ʱȡ����Сֵ����ʵ��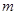 ��ȡֵ��ΧΪ�� ��
��ȡֵ��ΧΪ�� ��A��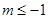 | B��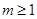 | C��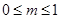 | D��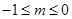 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 (x)=��x(x+1)������g(x)=f(logax)(0��a��1)�ĵ����ݼ������ǣ� ��
(x)=��x(x+1)������g(x)=f(logax)(0��a��1)�ĵ����ݼ������ǣ� ��| A��[��1,0] | B��[ ��+��),(0,1] ��+��),(0,1] |
C��[1,  ] ] | D��(����, ) ��( ) ��( ,+��) ,+��) |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A�������ޣ�0�� | B����0��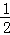 �� �� | C����0��1�� | D����0��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 �Ƕ�����
�Ƕ����� �ϵĺ������Ҷ�����ʵ��
�ϵĺ������Ҷ�����ʵ�� ������
������ ����
���� �����ֵΪ1����ʽ
�����ֵΪ1����ʽ �Ľ⼯Ϊ ���� .
�Ľ⼯Ϊ ���� .�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ��
�� Ϊʵ��������
Ϊʵ�������� ������
������ ���������������ú��������ԵĶ�����ʵ��
���������������ú��������ԵĶ�����ʵ�� ��ȡֵ��Χ��
��ȡֵ��Χ�� ��������ʽ
��������ʽ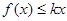 ��
��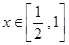 �н⣬��
�н⣬�� ��ȡֵ��Χ��
��ȡֵ��Χ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com