分析:(Ⅰ)由题意及所给的图形,可以A为原点,
,
,
的方向为X轴,Y轴,Z轴的正方向建立空间直角坐标系,设AB=a,给出图形中各点的坐标,可求出向量
与
的坐标,验证其数量积为0即可证出两线段垂直.
(II)由题意,可先假设在棱AA
1上存在一点P(0,0,t),使得DP∥平面B
1AE,求出平面B
1AE法向量,可法向量与直线DP的方向向量内积为0,由此方程解出t的值,若能解出,则说明存在,若不存在符合条件的t的值,说明不存在这样的点P满足题意.
(III)由题设条件,可求面夹二面角的两个平面的法向量,利用两平面的夹角为30°建立关于a的方程,解出a的值即可得出AB的长
解答: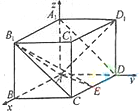
解:(I)以A为原点,
,
,
的方向为X轴,Y轴,Z轴的正方向建立空间直角坐标系,如图,
设AB=a,则A(0,0,0),D(0,1,0),D
1(0,1,1),E(
,1,0),B
1(a,0,1)
故
=(0,1,1),
=(-
,1,-1),
=(a,0,1),
=(
,1,0),
∵
•
=1-1=0
∴B
1E⊥AD
1;
(II)假设在棱AA
1上存在一点P(0,0,t),使得DP∥平面B
1AE.此时
=(0,-1,t).
又设平面B
1AE的法向量
=(x,y,z).
∵
⊥平面B
1AE,∴
⊥B
1A,
⊥AE,得
,取x=1,得平面B
1AE的一个法向量
=(1,-
,-a).
要使DP∥平面B
1AE,只要
⊥
,即有
•
=0,有此得
-at=0,解得t=
,即P(0,0,
),
又DP?平面B
1AE,
∴存在点P,满足DP∥平面B
1AE,此时AP=
(III)连接A
1D,B
1C,由长方体ABCD-A
1B
1C
1D
1及AA
1=AD=1,得AD
1⊥A
1D.
∵B
1C∥A
1D,∴AD
1⊥B
1C.
由(I)知,B
1E⊥AD
1,且B
1C∩B
1E=B
1.
∴AD
1⊥平面DCB
1A
1,
∴AD
1是平面B
1A
1E的一个法向量,此时
=(0,1,1).
设
与
所成的角为θ,则cosθ=
=
∵二面角A-B
1E-A
1的大小为30°,
∴|cosθ|=cos30°=
即
=
,解得a=2,即AB的长为2
点评:本题考查利用空间向量这一工具求二面角,证明线面平行及线线垂直,解题的关键是建立恰当的坐标系及空间位置关系与向量的对应,此类解题,方法简单思维量小,但计算量大,易因为计算错误导致解题失败,解题时要严谨,认真,利用空间向量求解立体几何题是近几年高考的热点,必考内容,学习时要好好把握

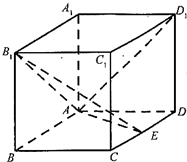 (2012•福建)如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点.
(2012•福建)如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点. 解:(I)以A为原点,
解:(I)以A为原点,

 (2012•福建)如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点.
(2012•福建)如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点. (2012•福建)如图,等边三角形OAB的边长为8
(2012•福建)如图,等边三角形OAB的边长为8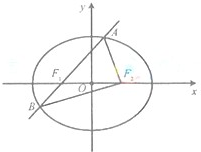 (2012•福建)如图,椭圆E:
(2012•福建)如图,椭圆E: