
【题目】在平面直角坐标系xOy中,已知曲线C的参数方程为![]() 为参数
为参数![]() ,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系.
,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系.
(1)求曲线C的极坐标方程;
(2)设直线l的极坐标方程为![]() ,若直线l与曲线C交于M,N两点,且
,若直线l与曲线C交于M,N两点,且![]() ,求直线l的直角坐标方程.
,求直线l的直角坐标方程.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|.
(1)若不等式f(x)≥|2x+1|1的解集为A,且![]() ,求实数t的取值范围;
,求实数t的取值范围;
(2)在(1)的条件下,若![]() ,证明:f(ab)>f(a)f(b).
,证明:f(ab)>f(a)f(b).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把分别写有1,2,3,4,5的五张卡片全部分给甲、乙、丙三个人,每人至少一张,且若分得的卡片超过一张,则必须是连号,那么不同的分法种数为______![]() 用数字作答
用数字作答![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校初中部共120名教师,高中部共180名教师,其性别比例如图所示,已知按分层抽样方法得到的工会代表中,高中部女教师有6人,则工会代表中男教师的总人数为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南昌市在2018年召开了全球VR产业大会,为了增强对青少年VR知识的普及,某中学举行了一次普及VR知识讲座,并从参加讲座的男生中随机抽取了50人,女生中随机抽取了70人参加VR知识测试,成绩分成优秀和非优秀两类,统计两类成绩人数得到如下的![]() 列联表:
列联表:
优秀 | 非优秀 | 总计 | |
男生 |
| 35 | 50 |
女生 | 30 |
| 70 |
总计 | 45 | 75 | 120 |
(1)确定![]() ,
,![]() 的值;
的值;
(2)试判断能否有90%的把握认为VR知识测试成绩优秀与否与性别有关;
附: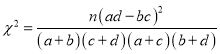
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,点E是棱
中,点E是棱![]() 的中点,点F是线段
的中点,点F是线段![]() 上的一个动点.有以下三个命题:
上的一个动点.有以下三个命题:
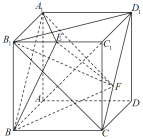
①异面直线![]() 与
与![]() 所成的角是定值;
所成的角是定值;
②三棱锥![]() 的体积是定值;
的体积是定值;
③直线![]() 与平面
与平面![]() 所成的角是定值.
所成的角是定值.
其中真命题的个数是( )
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com