
【题目】给出下列结论:
①下面程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的![]() ,
,![]() 分别为8,12,则输出的
分别为8,12,则输出的![]() ;
;

②若用样本数据0,-1,2,3来估计总体的标准差,则总体的标准差估计值为![]() ;
;
③命题:“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”;
”;
④已知正数![]() ,
,![]() 满足
满足![]() ,则
,则![]() 的最大值是
的最大值是![]() ;
;
⑤已知函数![]() 满足
满足![]() ,
,![]() ,且当
,且当![]() 时,
时,![]() .则
.则![]() 在区间
在区间![]() 为增函数.
为增函数.
其中结论正确的序号是______.
【答案】①②⑤
【解析】
①模拟程序运行即可判断;
②根据公式依次求出平均数、方程、标准差,由此即可判断;
③“![]() ”的否定为“
”的否定为“![]() ”,由此即可判断;
”,由此即可判断;
④由基本不等式化简得![]() ,则
,则![]() ,解出不等式即可判断;
,解出不等式即可判断;
⑤由题意知![]() 是奇函数,且关于
是奇函数,且关于![]() 对称,则
对称,则![]() 是周期
是周期![]() 的函数,从而得到在
的函数,从而得到在![]() 与
与![]() 两段的图象相同,由此即可判断.
两段的图象相同,由此即可判断.
解:①模拟程序运行,输入的![]() ,
,![]() ,满足
,满足![]() ,但不满足
,但不满足![]() ,故对
,故对![]() 重新赋值为
重新赋值为![]() ;满足
;满足![]() ,满足
,满足![]() ,故对
,故对![]() 重新赋值为
重新赋值为![]() ;不满足
;不满足![]() ,则输出的
,则输出的![]() ,故①正确;
,故①正确;
②样本的平均数![]() ,方差
,方差![]() ,故总体总体的标准差估计值为
,故总体总体的标准差估计值为![]() ,故②正确;
,故②正确;
③命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”,故③错误;
”,故③错误;
④已知正数![]() ,
,![]() ,由基本不等式化简得
,由基本不等式化简得![]() ,所以
,所以![]() ,解得
,解得![]() ,当且仅当
,当且仅当![]() 时等号成立,故④错误;
时等号成立,故④错误;
⑤由题意知![]() 是奇函数,且关于
是奇函数,且关于![]() 对称,则函数
对称,则函数![]() 是最小正周期
是最小正周期![]() 的函数,又当
的函数,又当![]() 时,
时,![]() ,则当
,则当![]() 时,
时,![]() 单调递增,由周期性知,在
单调递增,由周期性知,在![]() 与
与![]() 两段的图象相同,故⑤正确;
两段的图象相同,故⑤正确;
故答案为:①②⑤.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】某班级共有50名同学(男女各占一半),为弘扬传统文化,班委组织了“古诗词男女对抗赛”,将同学随机分成25组,每组男女同学各一名,每名同学均回答同样的五个不同问题,答对一题得一分,答错或不答得零分,总分5分为满分.最后25组同学得分如下表:
组别号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
男同学得分 | 5 | 4 | 5 | 5 | 4 | 5 | 5 | 4 | 4 | 4 | 5 | 5 | 4 |
女同学得分 | 4 | 3 | 4 | 5 | 5 | 5 | 4 | 5 | 5 | 5 | 5 | 3 | 5 |
分差 | 1 | 1 | 1 | 0 | -1 | 0 | 1 | -1 | -1 | -1 | 0 | 2 | -1 |
组别号 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
男同学得分 | 4 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 4 | 3 | 3 | |
女同学得分 | 5 | 3 | 4 | 5 | 4 | 3 | 5 | 5 | 3 | 4 | 5 | 5 | |
分差 | -1 | 0 | 0 | -1 | 0 | 1 | 0 | 0 | 2 | 0 | -2 | -2 | |
(I)完成![]() 列联表,并判断是否有90%的把握认为“该次对抗赛是否得满分”与“同学性别”有关;
列联表,并判断是否有90%的把握认为“该次对抗赛是否得满分”与“同学性别”有关;
(Ⅱ)某课题研究小组假设各组男女同学分差服从正态分布![]() ,首先根据前20组男女同学的分差确定
,首先根据前20组男女同学的分差确定![]() 和
和![]() ,然后根据后面5组同学的分差来检验模型,检验方法是:记后面5组男女同学分差与
,然后根据后面5组同学的分差来检验模型,检验方法是:记后面5组男女同学分差与![]() 的差的绝对值分别为
的差的绝对值分别为![]() ,若出现下列两种情况之一,则不接受该模型,否则接受该模型.①存在
,若出现下列两种情况之一,则不接受该模型,否则接受该模型.①存在![]() ;②记满足
;②记满足![]() 的i的个数为k,在服从正态分布
的i的个数为k,在服从正态分布![]() 的总体(个体数无穷大)中任意取5个个体,其中落在区间
的总体(个体数无穷大)中任意取5个个体,其中落在区间![]() 内的个体数大于或等于k的概率为P,
内的个体数大于或等于k的概率为P,![]() .
.
试问该课题研究小组是否会接受该模型.
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
参考公式和数据: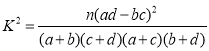
![]() ,
,![]() ;若
;若![]() ,有
,有![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】很多关于整数规律的猜想都通俗易懂,吸引了大量的数学家和数学爱好者,有些猜想已经被数学家证明,如“费马大定理”,但大多猜想还未被证明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是:对于每一个正整数,如果它是奇数,则将它乘以![]() 再加1;如果它是偶数,则将它除以
再加1;如果它是偶数,则将它除以![]() ;如此循环,最终都能够得到
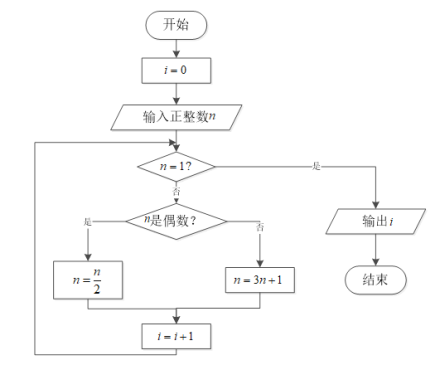
;如此循环,最终都能够得到![]() .下图为研究“角谷猜想”的一个程序框图.若输入
.下图为研究“角谷猜想”的一个程序框图.若输入![]() 的值为
的值为![]() ,则输出i的值为( )
,则输出i的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在![]() 上的偶函数
上的偶函数![]() 满足
满足![]() ,且在区间
,且在区间![]() 上是减函数,
上是减函数,![]() ,
,![]() 现有下列结论,其中正确的是:( )
现有下列结论,其中正确的是:( )
①![]() 的图象关于直线
的图象关于直线![]() 对称;②
对称;②![]() 的图象关于点
的图象关于点![]() 对称;③
对称;③![]() 在区间
在区间![]() 上是减函数;④
上是减函数;④![]() 在区间
在区间![]() 内有8个零点.
内有8个零点.
A.①③B.②④C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,全国各地区坚持稳中求进工作总基调,经济运行总体平稳,发展水平迈上新台阶,发展质量稳步上升,人民生活福祉持续增进,全年最终消费支出对国内生产总值增长的贡献率为57.8%.下图为2019年居民消费价格月度涨跌幅度:(同比![]() (本期数-去年同期数)/去年同期数
(本期数-去年同期数)/去年同期数![]() ,环比
,环比![]() (本期数-上期数)/上期数
(本期数-上期数)/上期数![]()
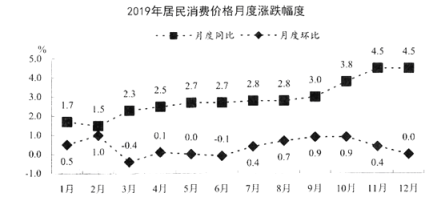
下列结论中不正确的是( )
A.2019年第三季度的居民消费价格一直都在增长
B.2018年7月份的居民消费价格比同年8月份要低一些
C.2019年全年居民消费价格比2018年涨了2.5%以上
D.2019年3月份的居民消费价格全年最低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,过原点
,过原点![]() 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆![]() 交于点
交于点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 、
、![]() .
.
(1)若![]() ,求点
,求点![]() 的横坐标;
的横坐标;
(2)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中心在原点的椭圆E的一个焦点与抛物线![]() 的焦点关于直线
的焦点关于直线![]() 对称,且椭圆E与坐标轴的一个交点坐标为
对称,且椭圆E与坐标轴的一个交点坐标为![]() .
.
(1)求椭圆E的标准方程;
(2)过点![]() 的直线l(直线的斜率k存在且不为0)交E于A,B两点,交x轴于点P点A关于x轴的对称点为D,直线BD交x轴于点Q.试探究
的直线l(直线的斜率k存在且不为0)交E于A,B两点,交x轴于点P点A关于x轴的对称点为D,直线BD交x轴于点Q.试探究![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() :
:![]() 的左右两个焦点,过
的左右两个焦点,过![]() 的直线与
的直线与![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 在第一象限),
在第一象限),![]() 的周长为8,
的周长为8,![]() 的离心率为
的离心率为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() ,
,![]() 为
为![]() 的左右顶点,直线
的左右顶点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com