练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    向量a＝(cos 15°，sin 15°)，b＝(sin 15°，cos 15°)，则|a－b|的值是     ．

    【解析】　由题设，|a|＝1，|b|＝1，

    a·b＝sin(15°＋15°)＝.

    ∴|a－b|2＝a2＋b2－2a·b＝1＋1－2×＝1.

    ∴|a－b|＝1.

    1

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：设计必修四数学苏教版 苏教版 题型：044

    设平面上有两向量a＝(cosα，sinα)(0°≤α＜360°)，b＝

    (1)求证：两向量a＋b与a－b垂直；

    (2)求当ka＋b与a－kb(k≠0)的模相等时α的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出以下四个命题：

    ①对任意两个向量a，b都有|a·b|＝|a||b|；

    ②若a，b是两个不共线的向量，且＝λ1a＋b，＝a＋λ2b(λ1，λ2∈R)，则A、B、C共线⇔λ1λ2＝－1；

    ③若向量a＝(cosα，sinα)，b＝(cosβ，sinβ)，则a＋b与a－b的夹角为90°.

    ④若向量a、b满足|a|＝3，|b|＝4，|a＋b|＝，则a，b的夹角为60°.

    以上命题中，错误命题的序号是________．

    查看答案和解析>>

    科目：高中数学 来源：2012人教A版高中数学必修四3.1两角和差的正弦余弦和正切公式（二）（解析版） 题型：解答题

    已知向量a＝(cosα，sinα)，b＝(cosβ，sinβ)，|a－b|＝.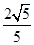

    (1)求cos(α－β)的值；

    (2)若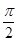－<β<0<α<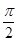，且sinβ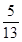＝－，求sinα的值．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设向量a＝（1+cosα，sinα），b=（1-cosβ，sinβ），c＝（1，0），α∈（0，π），β∈（π，2π），a与?c的夹角为θ1，b与c的夹角为θ2，且θ1-θ2?=，求sin的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设在平面上有两个向量a＝(cosα，sinα)(0°≤α<360°)，b＝(－，)．

    (1)求证：向量a＋b与a－b垂直；

    (2)当向量a＋b与a－b的模相等时，求α的大小．

    查看答案和解析>>

    同步练习册答案