
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据抽样方法的定义和特点即可判断;
②根据变量方差关系进行判断,
③用相关性系数r的意义去判断;
④根据随机变量k2的观测值k越大,“x与y有关系”的把握程度越大,判断④是否为真命题.
解答 解:①从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是系统抽样,故①错误,
②若数据x1,x2,x3,…xn的方差为1,则2x1,2x2,2x3,…,2xn的方差为4;故②错误
③根据线性相关系数r的意义可知,当两个随机变量线性相关性越强,r的绝对值越接近于1,故③正确;
④根据两个分类变量X与Y的随机变量k2的观测值k来说,k越大,判断“x与y有关”的把握程度越大,得④是假命题.故④错误,
故正确的是③,
故选:A
点评 本题考查命题的真假判断,涉及抽样方法的概念、相关系数的意义以及方差的关系,是一道基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
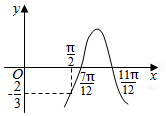
| A. | -$\frac{2}{3}$ | B. | -$\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | $\frac{33}{2}$ | C. | $\frac{35}{2}$ | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个圆锥被过顶点的平面截去了较小的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )
一个圆锥被过顶点的平面截去了较小的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )| A. | $\frac{\sqrt{2}}{3}$+$\frac{\sqrt{2}}{2}$π | B. | $\sqrt{2}$+$\frac{\sqrt{2}}{2}$π | C. | $\sqrt{2}$+$\frac{3\sqrt{2}}{2}$π | D. | 2$\sqrt{2}$+3$\sqrt{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 6 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com