
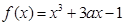 ,
,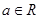 .
. (Ⅰ)若函数
(Ⅰ)若函数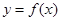 的图象在
的图象在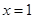 处的切线与直线
处的切线与直线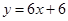 平行,求实数
平行,求实数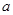 的值;
的值;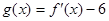 ,对满足
,对满足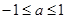 的一切
的一切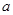 的值,都有
的值,都有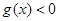 成立,求实数
成立,求实数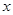 的取值范围;
的取值范围;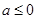 时,请问:是否存在整数
时,请问:是否存在整数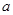 的值,使方程
的值,使方程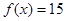 有且只有一个实根?若存在,求出整数
有且只有一个实根?若存在,求出整数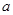 的值;否则,请说明理由.
的值;否则,请说明理由.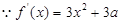 ..........(1分)
..........(1分)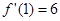 ........(2分)
........(2分)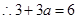
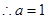 ...........(3分)
...........(3分)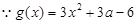
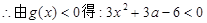 .......(4分)
.......(4分)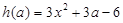 ,即
,即 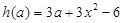 则依题意:对满足
则依题意:对满足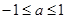 的一切
的一切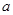 的值,都有
的值,都有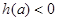
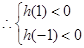 ,即
,即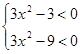
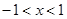 ......................(6分)
......................(6分)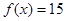 有且只有一个实根即为函数
有且只有一个实根即为函数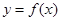 的图象与直线
的图象与直线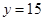 只有一个公共点
只有一个公共点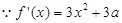
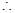 (1)若
(1)若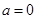 ,则
,则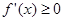 ,
,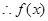 在实数集R上单调递增
在实数集R上单调递增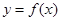 的图象与直线
的图象与直线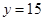 只有一个公共点......(8分)
只有一个公共点......(8分)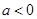 ,则
,则 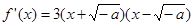 ..........(9分)
..........(9分)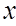 | 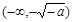 | 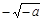 | 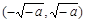 | 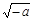 | 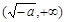 |
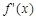 |  + + | 0 | 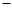 | 0 | 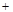 |
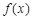 |    | 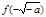 |  | 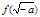 |  |
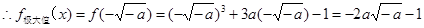
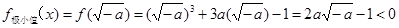
 依题意,必须满足
依题意,必须满足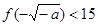 ,即
,即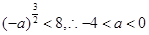
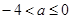 ...................(11分)
...................(11分)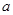 是整数,
是整数,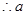 可取
可取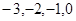 所以,存在整数
所以,存在整数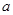 的值为
的值为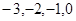 ,使方程
,使方程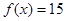 有且只有一个实根
有且只有一个实根

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源:不详 题型:解答题
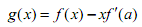 ,其中
,其中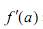 表示函数f(x)在
表示函数f(x)在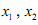 ,且
,且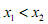 ,证明:
,证明: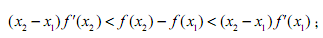
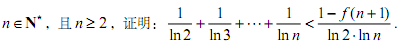
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,
,  .
.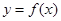 在
在 上是单调函数,求
上是单调函数,求 的取值范围;
的取值范围; ,使得函数
,使得函数 在区间
在区间 内有两个不同的零点?若存在,请求出
内有两个不同的零点?若存在,请求出 的取值范围;若不存在,请说明理由
的取值范围;若不存在,请说明理由查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com