Question

在四边形ABCD中，“∃λ∈R，使得AB=λDC，AD=λBC”是“四边形ABCD为平行四边形”的（　　）

	A．	充分而不必要条件	B．	必要而不充分条件
	C．	充分必要条件	D．	既不充分也不必要条件

Answer 1

考点：

必要条件、充分条件与充要条件的判断．

专题：

证明题．

分析：

根据平行四边形的判定定理：两组对边分别平行的四边形是平行四边形和必要条件、充分条件与充要条件的定义进行判断即可．

解答：

解：由在四边形ABCD中，“∃λ∈R，使得AB=λDC，AD=λBC”，不能得出AB∥DC，AD∥BC，

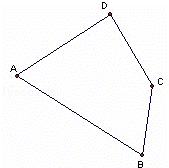
如图，AB=2DC，AD=2BC，不得到四边形ABCD为平行四边形．

也就不得到四边形ABCD为平行四边形，

反之，由四边形ABCD为平行四边形，得到AB=DC，AD=BC，从而有：∃λ=1∈R，使得AB=λDC，AD=λBC，

故在四边形ABCD中，“∃λ∈R，使得AB=λDC，AD=λBC”是“四边形ABCD为平行四边形”的必要而不充分条件．

故选B．

点评：

本题主要考查对平行四边形的判定定理，必要条件、充分条件与充要条件的判断，能灵活运用平行四边形的判定进行证明是解此题的关键，此题是一个比较综合的题目．