
���� ��1������֪��$\frac{1}{{a}_{n}}-\frac{1}{{a}_{n-1}}$=3���ɴ˵õ�����{$\frac{1}{{a}_{n}}$}������Ϊ1������Ϊ3�ĵȲ����У�
��2�����bn=$\frac{1}{{2}^{n}•{a}_{n}}$=$\frac{1}{{2}^{n}•\frac{1}{3n-2}}$=$\frac{3n-2}{{2}^{n}}$���ɴ����ô�λ��������������{bn}��ǰn���Sn��
��3��ԭ����ȼ���$�ˡ�\frac{��3n+1����3n-2��}{3n-3}$������n��2��������������ɴ�������˵�ȡֵ��Χ��
��� �⣺��1����������{an}�У�a1=1��3an•an-1+an-an-1=0��n��2��n��N*����
��$\frac{1}{{a}_{n}}-\frac{1}{{a}_{n-1}}$=3���֡�$\frac{1}{{a}_{1}}$=1��
������{$\frac{1}{{a}_{n}}$}������Ϊ1������Ϊ3�ĵȲ����У�
��2��������{$\frac{1}{{a}_{n}}$}������Ϊ1������Ϊ3�ĵȲ����У�
��$\frac{1}{{a}_{n}}$=1+��n-1����3=3n-2����an=$\frac{1}{3n-2}$��
��bn=$\frac{1}{{2}^{n}•{a}_{n}}$=$\frac{1}{{2}^{n}•\frac{1}{3n-2}}$=$\frac{3n-2}{{2}^{n}}$��
��${S}_{n}=\frac{1}{2}+\frac{4}{{2}^{2}}+\frac{7}{{2}^{3}}+��+\frac{3n-2}{{2}^{n}}$����
$\frac{1}{2}{S}_{n}$=$\frac{1}{{2}^{2}}+\frac{4}{{2}^{3}}+\frac{7}{{2}^{4}}+��+\frac{3n-2}{{2}^{n+1}}$����
��-�ڣ��ã�$\frac{1}{2}{S}_{n}^{\;}$=$\frac{1}{2}+\frac{3}{{2}^{2}}+\frac{3}{{2}^{3}}+��+\frac{3}{{2}^{n}}-\frac{3n-2}{{2}^{n+1}}$
=$\frac{1}{2}+\frac{\frac{3}{4}��1-\frac{1}{{2}^{n-1}}��}{1-\frac{1}{2}}-\frac{3n-2}{{2}^{n+1}}$��
��Sn=4-��3n+4��•��$\frac{1}{2}$��n��
��3����an=$\frac{1}{3n-2}$�����an+$\frac{1}{{a}_{n+1}}$�ݦˣ���������$�ˣ�1-\frac{1}{3n-2}����3n+1$��
��$�ˡ�\frac{��3n+1����3n-2��}{3n-3}$��ԭ����ȼ��ڸ�ʽ������n��2�������������
��${C}_{n}=\frac{��3n+1����3n-2��}{3n-3}$��
��${C}_{n+1}-{C}_{n}=\frac{��3n+1����3n-4��}{3n��n-1��}��0$����Cn+1��Cn��
��Cn����СֵΪC2=$\frac{28}{3}$����˵�ȡֵ��Χ�ǣ�-�ޣ�$\frac{28}{3}$]��
���� ���⿼��Ȳ����е��жϣ��������е�ǰn��͵�������ʵ����ȡֵ��Χ�������е��⣬����ʱҪ�������⣬ע���λ������͵ȼ�ת��˼��ĺ������ã�


 �±�Сѧ��Ԫ�Բ���ϵ�д�
�±�Сѧ��Ԫ�Բ���ϵ�д� �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
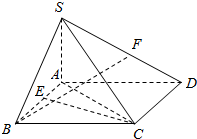 ��ͼ��������S-ABCD�У�SA=SB������ABCD�����Σ��ҡ�ABC=60�㣬��E��F�ֱ���AB��SD���е㣮
��ͼ��������S-ABCD�У�SA=SB������ABCD�����Σ��ҡ�ABC=60�㣬��E��F�ֱ���AB��SD���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5��10��15��20��25 | B�� | 5��12��31��39��57 | C�� | 5��17��29��41��53 | D�� | 5��15��25��35��45 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��-1�� | B�� | ��-2��0�� | C�� | ��-3��1�� | D�� | ��-1��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com