
【题目】以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】将函数f(x)=sinωx(ω>0)的图象向左平移 ![]() 个单位得到函数g(x)的图象,若函数g(x)的图象关于直线x=ω对称且在区间(﹣ω,ω)内单调递增,则ω的值为( )
个单位得到函数g(x)的图象,若函数g(x)的图象关于直线x=ω对称且在区间(﹣ω,ω)内单调递增,则ω的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四边形ABEF是正方形,且平面ABEF⊥平面ABCD,M为AF的中点, (I)求证:AC⊥BM;
(II)求异面直线CE与BM所成角的余弦值.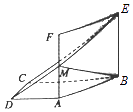
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四边形ABEF是正方形.将正方形ABEF沿AB折起到四边形ABE1F1的位置,使平面ABE1F1⊥平面ABCD,M为AF1的中点,如图2. 
(I)求证:AC⊥BM;
(Ⅱ)求平面CE1M与平面ABE1F1所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且(c+b)(sinC﹣sinB)=a(sinA﹣sinB).若c=2 ![]() ,则a2+b2的取值范围是 .
,则a2+b2的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)为奇函数,且在(﹣∞,0)内是减函数,f(﹣2)=0,则xf(x)<0的解集为( )
A.(﹣1,0)∪(2,+∞)
B.(﹣∞,﹣2)∪(0,2)
C.(﹣∞,﹣2)∪(2,+∞)
D.(﹣2,0)∪(0,2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为 ![]() 的正方形
的正方形 ![]() (及其内部)绕
(及其内部)绕 ![]() 旋转一周形成圆柱,如图,
旋转一周形成圆柱,如图, ![]() 长为
长为 ![]() ,
, ![]() 长为
长为 ![]() ,其中
,其中 ![]() 与
与 ![]() 在平面
在平面 ![]() 的同侧.
的同侧.
(1)求三棱锥 ![]() 的体积;
的体积;
(2)求异面直线 ![]() 与
与 ![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com