
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)单调减区间是![]() ,单调增区间是
,单调增区间是![]() .(2)
.(2)  .
.
【解析】试题分析:
(1)当![]() 时,
时, ![]() ,
,  ,结合导函数与原函数之间的关系可得
,结合导函数与原函数之间的关系可得![]() 的单调减区间是
的单调减区间是![]() ,单调增区间是
,单调增区间是![]() .
.
(2)分类讨论:
①当![]() 时,符合题意;
时,符合题意;
②当![]() 时,
时, ![]() ,由题意可得存在
,由题意可得存在![]() ,使得
,使得![]() ,即
,即![]() ,据此可得a
,据此可得a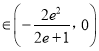 .
.
据此可得,实数![]() 的取值范围
的取值范围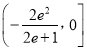
试题解析:
(1)由题意得![]() ,当
,当![]() 时,
时,
![]() ,
, 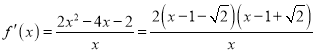
∴当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
∴![]() 的单调减区间是
的单调减区间是![]() ,单调增区间是
,单调增区间是![]() .
.
(2)①当![]() 时,
时, ![]() ,显然符合题意;
,显然符合题意;
②当![]() 时,
时, ![]() ,令
,令![]() ,
, ![]() 恒成立.
恒成立.
∴该方程有两个不同实根,且一正一负,即存在![]() ,使得
,使得![]() ,即
,即![]() ,∴当
,∴当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
由于![]() 在
在![]() 上是增函数,∴
上是增函数,∴![]() .
.
由于![]() 得
得![]() ,设
,设![]() ,则
,则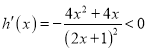 .
.
∴函数![]() 在
在![]() 上单调递减,∴
上单调递减,∴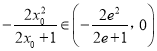 .
.
综上所述,实数![]() 的取值范围
的取值范围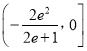


科目:高中数学 来源: 题型:
【题目】设m个正数a1 , a2 , …,am(m≥4,m∈N*)依次围成一个圆圈.其中a1 , a2 , a3 , …ak﹣1 , ak(k<m,k∈N*)是公差为d的等差数列,而a1 , am , am﹣1 , …,ak+1 , ak是公比为2的等比数列.
(1)若a1=d=2,k=8,求数列a1 , a2 , …,am的所有项的和Sm;
(2)若a1=d=2,m<2015,求m的最大值;
(3)是否存在正整数k,满足a1+a2+…+ak﹣1+ak=3(ak+1+ak+2+…+am﹣1+am)?若存在,求出k值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC
(1)求三棱锥D-ABC的体积
(2)求证:平面DAC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN=![]() CA,求证:MN∥平面DEF
CA,求证:MN∥平面DEF

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某智能手机制作完成之后还需要依次通过三道严格的审核程序,第一道审核、第二道审核、第三道审核通过的概率分别为![]() ,
,![]() ,
,![]() ,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.
,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.
(1)求审核过程中只通过两道程序的概率;
(2)现有3部该智能手机进入审核,记这3部手机可以出厂销售的部数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算下面各题
(1)求过点A(2,3),且垂直于直线3x+2y﹣1=0的直线方程;
(2)已知直线l过原点,且点M(5,0)到直线l的距离为3,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20为市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下:
甲校:58,66,71,58,67,72,82,92,83,86,67,59,86,72,78,59,68,69,73,81;
乙校:90,80,73,65,67,69,81,85,82,88,89,86,86,78,98,95,96,91,76,69,.
检查组将成绩分成了四个等级:成绩在区间![]() 的为
的为![]() 等,在区间
等,在区间![]() 的为
的为![]() 等,在区间
等,在区间![]() 的为
的为![]() 等,在区间
等,在区间![]() 为
为![]() 等.
等.
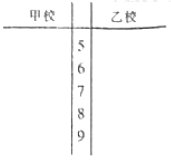
(1)请用茎叶图表示上面的数据,并通过观察茎叶图,对两所学校办学的社会满意度进行比较,写出两个统计结论;
(2)根据所给数据,以事件发生的频率作为相应事件发生的概率,求乙校得分的等级高于甲校得分的等级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() 点,动圆
点,动圆![]() 与直线
与直线![]() 相切,并且与圆
相切,并且与圆![]() 相外切,
相外切,
(1)求动圆的圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若过原点且倾斜角为![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 两点,问是否存在以
两点,问是否存在以![]() 为直径的圆经过点
为直径的圆经过点![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,
的左、右焦点, ![]() 为坐标原点,点
为坐标原点,点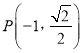 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)圆![]() 是以
是以![]() 为直径的圆,一直线
为直径的圆,一直线![]() 与圆
与圆![]() 相切,并与椭圆交于不同的两点
相切,并与椭圆交于不同的两点![]() 、
、![]() ,当
,当![]() ,且满足
,且满足![]() 时,求
时,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com