练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知sinαcosβ=1，则数学公式=________．


    分析：由题意及正弦函数和余弦函数的值域可得sinα=cosβ=1，或sinα=cosβ=-1，求出α和β的值，运算可得
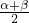
    =（n+k）π+，则得=．
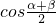
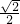
    解答：∵-1≤sinα≤1，-1≤cosβ≤1，sinαcosβ=1，∴sinα=cosβ=1，或sinα=cosβ=-1，
    ∴α=2kπ+，β=2nπ，或 α=2kπ-，β=2nπ+π，k，n∈z．
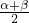
    故α+β=（2n+2k）π+，∴=（n+k）π+，∴则=，
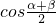
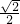
    故答案为：．
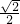
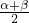
    点评：本题考查两角和差的余弦公式的应用，正弦函数和余弦函数的值域，求得 =（n+k）π+，是解题的难点和关键．
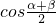    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知sinα+cosα=
    7
    13
    （0＜α＜π），则tanα=（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知sinα-cosα=
    		2
    ，求sin2α的值（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知sinα+cosα=
    15
    且0＜α＜π，求值：
    （1）sin3α-cos3α；　　
    （2）tanα．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知sinθ+cosθ=
    		2
    2
    （0＜θ＜π），则cos2θ的值为
    -
    		3
    2
    -
    		3
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知sinθ+cosθ=
    15
    ，0＜θ＜π    ，求下列各式的值：
    （1）sinθ•cosθ
    （2）sinθ-cosθ
    （3）tanθ

    查看答案和解析>>

    同步练习册答案