
(满分14分)已知二次函数f(x)的二次项系数为a,且不等式f(x)>-2x的解集为(1,3).
(1)若方程f(x)+6a=0有两个相等的根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求实数a的取值范围.
解:本题主要考查二次函数、方程的根与系数关系,考查运用数学知识解决问题的能力.
(1)∵f(x)+2x>0的解集为(1,3).
∴f(x)+2x=a(x-1)(x-3),且a<0,因而
f(x)=a(x-1)(x-3)-2x=ax2-(2+4a)x+3a. ①
由方程f(x)+6a=0,得ax2-(2+4a)x+9a=0.②
∵方程②有两个相等的根,∴Δ=[-(2+4a)]2-4a·9a=0,即5a2-4a-1=0.
解得a=1或a=-. 由于a<0,舍去a=1,将a=-代入①得
f(x)的解析式为f(x)=-x2-x-.
(2)由f(x)=ax2-2(1+2a)x+3a=a2-
及a<0,可得f(x)的最大值为-. 由
解得a<-2-或-2+<a<0.
故当f(x)的最大值为正数时,实数a的取值范围是(-∞,-2-)∪(-2+,0).
【解析】略


科目:高中数学 来源:2010-2011学年梅州市曾宪梓中学高二第二学期期末考试数学(文) 题型:解答题
(满分14分)已知二次函数f(x)的二次项系数为a,且不等式f(x)>-2x的解集为(1,3).
(1)若方程f(x)+6a=0有两个相等的根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届福建省三明市高一第一学期联合命题考试数学 题型:解答题
(本小题满分14分)
已知二次函数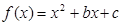 的图象过点
的图象过点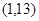 ,且函数对称轴方程为
,且函数对称轴方程为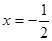 .
.
(Ⅰ)求函数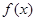 的解析式;
的解析式;
(Ⅱ)设函数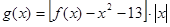 ,求
,求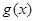 在区间
在区间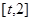 上的最小值
上的最小值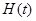 ;
;
(Ⅲ)探究:函数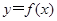 的图象上是否存在这样的点,使它的横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
的图象上是否存在这样的点,使它的横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013届广东省高二第一学期期末考试文科数学 题型:解答题
(本小题满分14分)
已知二次函数 (
( )的导函数
)的导函数
的图象如图所示:
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)令 ,求
,求 在
在 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中数学 来源:2014届四川省高一3月月考理科数学试卷 题型:解答题
(本小题满分14分)已知二次函数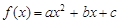 满足:①
满足:①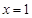 时有极值;②图象过点
时有极值;②图象过点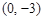 ,且在该点处的切线斜率为
,且在该点处的切线斜率为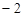 .
.
(I) 求f(x)的解析式;
(II)若曲线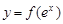 上任意一点的切线的斜率恒大于
上任意一点的切线的斜率恒大于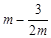 ,求
,求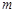 的取值范围;
的取值范围;
(Ⅲ)当非零实数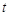 满足什么条件时,函数
满足什么条件时,函数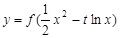 的图象与坐标轴没有公共点?
的图象与坐标轴没有公共点?
查看答案和解析>>
科目:高中数学 来源:2010-2011年福建省高二下学期期中考试文科数学 题型:解答题
(本小题满分14分)
已知二次函数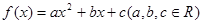 ,且同时满足下列条件:
,且同时满足下列条件:
①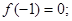 ② 对任意的实数
② 对任意的实数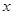 ,都有
,都有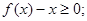
③ 当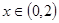 时,有
时,有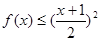 。
。
(1)求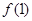 ;
;
(2)求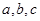 的值;
的值;
(3)当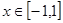 时,函数
时,函数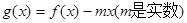 是单调函数,求
是单调函数,求 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com