
【题目】已知圆![]() 经过
经过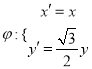 变换后得曲线
变换后得曲线![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() 为曲线
为曲线![]() 上两点,
上两点, ![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率分别为
的斜率分别为![]() 且
且![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值及此时直线
截得弦长的最大值及此时直线![]() 的方程.
的方程.
【答案】(1)![]() (2)直线
(2)直线![]() 被圆
被圆![]() :
: ![]() 截得弦长的最大值为
截得弦长的最大值为![]() ,
,
此时,直线![]() 的方程为
的方程为![]()
【解析】试题分析:(1)根据转移法求轨迹方程:将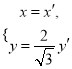 代入
代入![]() 得
得![]() ,化简可得
,化简可得![]() (2)先根据斜率公式表示
(2)先根据斜率公式表示![]() 为
为![]() ,再联立直线方程
,再联立直线方程![]() 与椭圆方程,结合韦达定理可得
与椭圆方程,结合韦达定理可得![]() ,由垂径定理得圆心到直线
,由垂径定理得圆心到直线![]() 的距离
的距离![]() 最小时,弦长最大,而
最小时,弦长最大,而![]() ,因此当
,因此当![]() 时,弦长最大,可得此时直线
时,弦长最大,可得此时直线![]() 的方程.
的方程.
试题解析:解:(Ⅰ)将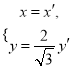 代入
代入![]() 得
得![]() ,
,
化简得![]() ,即
,即![]() 为曲线
为曲线![]() 的方程.
的方程.
(Ⅱ)设![]() ,
, ![]() ,直线
,直线![]() 与圆
与圆![]() :
: ![]() 的交点为
的交点为![]() .
.
当直线![]() 轴时,
轴时, ![]() ,
,
由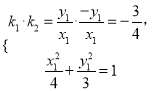 得
得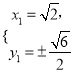 或
或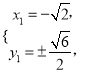
此时可求得![]() .
.
当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() ,
,
联立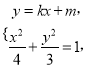 消
消![]() 得
得![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
所以![]()
![]() ,
,
由![]() 得
得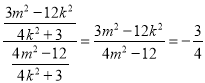 ,
, ![]()
此时![]() .
.
圆![]() :
: ![]() 的圆心到直线
的圆心到直线![]() 的距离为
的距离为![]() ,
,
所以![]() ,
,
得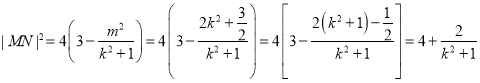 ,
,
所以当![]() 时,
时, ![]() 最大,最大值为
最大,最大值为![]() ,
,
综上,直线![]() 被圆
被圆![]() :
: ![]() 截得弦长的最大值为
截得弦长的最大值为![]() ,
,
此时,直线![]() 的方程为
的方程为![]() .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:
【题目】如图,已知直线![]() 关于直线
关于直线![]() 对称的直线为
对称的直线为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 分别交于点
分别交于点![]() 、
、![]() 和
和![]() 、
、![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)当![]() 变化时,试问直线
变化时,试问直线![]() 是否恒过定点? 若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
是否恒过定点? 若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且当x>0时,函数f(x)的解析式为![]() .
.
(1)求当x<0时函数f(x)的解析式;
(2)用定义证明f(x)在(0,+∞)上的是减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD中,
(1)点E是AB的中点,点F是BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.求证:A′D⊥EF.
(2)当BE=BF=![]() BC时,求三棱锥A′﹣EFD体积.
BC时,求三棱锥A′﹣EFD体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理财公司有两种理财产品![]() 和
和![]() .这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
.这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]()
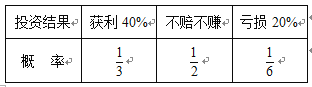
产品![]() (其中
(其中![]() )
)
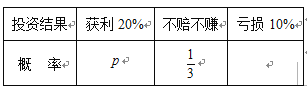
(Ⅰ)已知甲、乙两人分别选择了产品![]() 和产品
和产品![]() 进行投资,如果一年后他们中至少有一人获利的概率大于
进行投资,如果一年后他们中至少有一人获利的概率大于![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅱ)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品![]() 和产品
和产品![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AA1=AB=2,AD=1,E,F,G分别是DD1 , AB,CC1的中点,则异面直线A1E与GF所成角为( ) 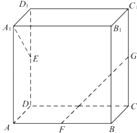
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com