
| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
分析 根据f(x)是定义在R上的奇函数,满足f(-$\frac{3}{2}$+x)=f($\frac{3}{2}$+x),可得函数的周期为3,再由奇函数的性质结合已知可得f($-\frac{3}{2}$)=f(-1)=f(0)=f(1)=f($\frac{3}{2}$)=0,利用周期性可得函数f(x)在区间[0,6]上的零点个数.
解答 解:∵f(x)是定义在R上的奇函数,满足f(-$\frac{3}{2}$+x)=f($\frac{3}{2}$+x),
∴f($-\frac{3}{2}+x+\frac{3}{2}$)=f($\frac{3}{2}+x+\frac{3}{2}$),可得f(x+3)=f(x),
函数f(x)的周期为3,
∵当x∈[0,$\frac{3}{2}$]时,f(x)=ln(x2-x+1),
令f(x)=0,则x2-x+1=1,解得x=0或1,
又∵函数f(x)是定义域为R的奇函数,
∴在区间∈[-$\frac{3}{2}$,$\frac{3}{2}$]上,有f(-1)=-f(1)=0,f(0)=0.
由f(-$\frac{3}{2}$+x)=f($\frac{3}{2}$+x),取x=0,得
f(-$\frac{3}{2}$)=f($\frac{3}{2}$),得f($\frac{3}{2}$)=f(-$\frac{3}{2}$)=0,
∴f(-1)=f(1)=f(0)=f($\frac{3}{2}$)=f(-$\frac{3}{2}$)=0.
又∵函数f(x)是周期为3的周期函数,
∴方程f(x)=0在区间[0,6]上的解有0,1,$\frac{3}{2}$,2,3,4,$\frac{9}{2}$,5,6.
共9个,
故选:D.
点评 本题考查根的存在性及根的个数判断,考查抽象函数周期性的应用,考查逻辑思维能力与推理论证能力,属于中档题.


科目:高中数学 来源: 题型:选择题

| A. | f(x)=xsinx | B. | f(x)=xcosx-sinx | C. | f(x)=xcosx | D. | f(x)=xcosx+sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
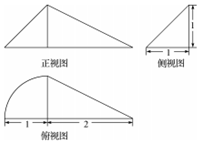
| A. | $\frac{π}{6}+\frac{1}{3}$ | B. | $\frac{π}{12}+1$ | C. | $\frac{π}{12}+\frac{1}{3}$ | D. | $\frac{π}{4}+\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n | B. | 2n | C. | n2 | D. | nn |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
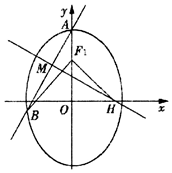 已知椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦点分别为F1,F2,上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=$\frac{1}{2}$.
已知椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的上、下焦点分别为F1,F2,上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x0∈R,sinx0>1”的否定是“?x∈R,sinx>1” | |
| B. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” | |
| C. | 在△ABC中,A>B是sinA>sinB的充分不必要条件 | |
| D. | 若p∧(¬q)为假,p∨(¬q)为真,则p,q同真或同假 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com