Question

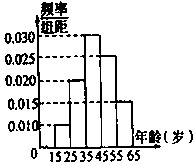
19．某市电视台为了宣传，举办问答活动，随机对该市15至65岁的人群进行抽样，频率分布直方图及回答问题统计结果如表所示：

组号	分组	回答正确 的人数	回答正确的人数 占本组的概率
第1组	[15，25）	5	0.5
第2组	[25，35）	a	0.9
第3组	[35，45）	27	x
第4组	[45，55）	b	0.36
第5组	[55，65）	3	y

（1）分别求出a，b，x，y的值；
（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，则第2，3，4组每组应各抽取多少人？
（3）在（2）的前提下，电视台决定在所抽取的6人中随机抽取3人颁发幸运奖，求：所抽取的人中第3组至少有1人获得幸运奖的概率．

Answer 1

分析 （1）先求出第1组人数为100，从而得到n=1000，由此能求出求出a，b，x，y的值．
（2）第2，3，4组回答正确的人的比为2：3：1，由此能求出第2，3，4组每组应各抽取的人数．
（3）记抽取的6人中，第2组的记为a₁，a₂，第3组的记为b₁，b₂，b₃，第4组的记为c，由此利用列举法能求出所抽取的人中第3组至少有1人获得幸运奖的概率．

解答 解：（1）第1组人数5÷0.05=100，
所以n=100÷0.1=1000，
第2组人数1000×0.2=200，所以a=200×0.9=180，
第3组人数1000×0.3=300，所以x=270÷300=0.9，
第4组人数1000×0.25=250，所以b=250×0.36=90，
第5组人数1000×0.15=150，所以y=3÷150=0.02．
（2）第2，3，4组回答正确的人的比为180：270：90=2：3：1，
从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，
所以第2，3，4组每组应各依次抽取2人，3人，1人．
（3）记抽取的6人中，第2组的记为a₁，a₂，第3组的记为b₁，b₂，b₃，第4组的记为c，
则从6名学生中任取3名的所有可能的情况有20种，它们是：$\begin{array}{l}（{a_1}，{a_2}，{b_1}），（{a_1}，{a_2}，{b_2}），（{a_1}，{a_2}，{b_3}），（{a_1}，{a_2}，c），（{a_1}，{b_1}，{b_2}），（{a_1}，{b_1}，{b_3}），（{a_1}，{b_1}，c），（{a_1}，{b_2}，{b_3}），（{a_1}，{b_2}，c），\\（{a_1}，{b_3}，c），（{a_2}，{b_1}，{b_2}），（{a_2}，{b_1}，{b_3}），（{a_2}，{b_1}，c），（{a_2}，{b_2}，{b_3}），（{a_2}，{b_2}，c），（{a_2}，{b_3}，c），（{b_1}，{b_2}，{b_3}），（{b_1}，{b_2}，c），\\（{b_1}，{b_3}，c），（{b_2}，{b_3}，c）\end{array}$
其中记“第3组至少有1人”为事件A，则A的对立事件是“第3组的没有选到”，
其基本事件个数是1个，即（a₁，a₂，c），
故所抽取的人中第3组至少有1人获得幸运奖的概率为$P（A）=1-P（\overline A）=1-\frac{1}{20}=\frac{19}{20}$．

点评 本题考查频率分布直方图、分层抽样的应用，考查概率的求法，是基础题，解题时要认真审题，注意列举法的合理运用．