{-
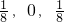
}
分析:令t=x-

=

=

,通过分类讨论,去掉绝对值符号,得到分段函数表达式,作出其图象即可得到答案.
解答:t=x-

=

=

①若x<-1,t<0,y=|x+

|-|x-

|=(-x-

)-(

-x)=-

;
②若-1<x<0,t>0,y=|x+

|-|x-

|=(-x-

)-(x-

)=-2x;
③若0<x<1,t<0,则y=|x+

|-|x-

|=(x+

)-(

-x)=2x;
④若x>1即 t>0,则曲线y=|x+

|-|x-

|=(x+

)-(x-

)=

.
∴y=
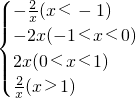
,作图如右:

由于直线y=kx+1经过定点A(0,1),当过A点的直线m与曲线y=-

相切时,直线m与曲线y=|x+

|-|x-

|有四个公共点,
设切点坐标为:(x
0,y
0),则k=(-

)′
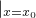
=
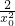
,
∴y
0=-

=kx
0+1=
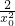
•x
0+1,解得;x
0=-4,
∴k=
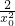
=

;
同理,可得当直线n与曲线y=

相切时,直线n与曲线y=|x+

|-|x-

|有四个公共点,可求得直线n的斜率为k′=-

;
当过A点的直线l∥x轴,即其斜率为0时,直线l与曲线y=|x+

|-|x-

|有四个公共点;
综上所述,实数k的取值范围是{

,0,-

}.
故答案为:{

,0,-

}.
点评:本题考查带绝对值的函数,关键在于去绝对值符号,难点在于分类讨论去绝对值符号,考查作图能力,属于难题.

 |-|x-
|-|x- |有四个公共点,则实数k的取值范围是________.
|有四个公共点,则实数k的取值范围是________.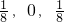 }
} =
= =
= ,通过分类讨论,去掉绝对值符号,得到分段函数表达式,作出其图象即可得到答案.
,通过分类讨论,去掉绝对值符号,得到分段函数表达式,作出其图象即可得到答案. =
= =
=
 |-|x-
|-|x- |=(-x-
|=(-x- )-(
)-( -x)=-
-x)=- ;
; |-|x-
|-|x- |=(-x-
|=(-x- )-(x-
)-(x- )=-2x;
)=-2x; |-|x-
|-|x- |=(x+
|=(x+ )-(
)-( -x)=2x;
-x)=2x;  |-|x-
|-|x- |=(x+
|=(x+ )-(x-
)-(x- )=
)= .
.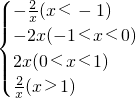 ,作图如右:
,作图如右:
 相切时,直线m与曲线y=|x+
相切时,直线m与曲线y=|x+ |-|x-
|-|x- |有四个公共点,
|有四个公共点, )′
)′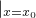 =
=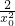 ,
, =kx0+1=
=kx0+1=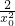 •x0+1,解得;x0=-4,
•x0+1,解得;x0=-4,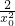 =
= ;
; 相切时,直线n与曲线y=|x+
相切时,直线n与曲线y=|x+ |-|x-
|-|x- |有四个公共点,可求得直线n的斜率为k′=-
|有四个公共点,可求得直线n的斜率为k′=- ;
; |-|x-
|-|x- |有四个公共点;
|有四个公共点; ,0,-
,0,- }.
}. ,0,-
,0,- }.
}.

 阅读快车系列答案
阅读快车系列答案 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.