练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知椭圆+=1(a＞b＞0)内有一点A,F1为左焦点,F2为右焦点,在椭圆上求一点P,使|PF1|+|PA|取得最值.

    思路解析：求曲线上一动点与某定点距离之和的最值,往往是利用几何变换,使得P、F1、A三点共线，或构建三角形，利用三角形的性质确定大小，进而确定最值的.

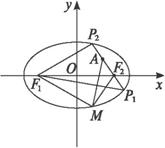
    解：如图，设AF2与椭圆交于P1、P2两点，点M是椭圆上不同于P1、P2的任意一点.

    根据椭圆的定义,得|P1F1|+|P1F2|=2a,

     ∴|P1F1|+|P1A|=|P1F1|+|P1F2|+|F2A|=2a+|F2A|.

    在△AMF2中，|MA|＜|MF2|+|F2A|，

    ∴|MF1|+|MA|＜|MF1|+|MF2|+|F2A|=2a+|F2A|.

    ∵点M是椭圆上任意一点，∴|MF1|+|MA|＜2a+|F2A|,

    ∴|MF1|+|MA|＜|P1F1|+|P1A|.

    点P1是使|PF1|+|PA|取得最大值的点.

    同理,|P2F1|+|P2A|=|P2F1|+|P2F2|-|AF2|=2a-|AF2|.

    在△AMF2中，|MA|＞|MF2|-|AF2|.

    ∴|MF1|+|MA|＞|MF1|+|MF2|-|AF2|=2a-|AF2|.

    ∴|MF1|+|MA|＞|P2F1|+|P2A|.

    ∴点P2是使|PF1|+|PA|取得最小值的点.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知椭圆=1(a＞b＞0)的左焦点到右准线的距离为,中心到准线的距离为，则椭圆的方程为

    A.+y2=1                                                     B.+y2=1

    C.=1                                                  D. =1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆=1(a＞b＞0)的两个焦点为F1、F2，过F2作垂直于x轴的直线与椭圆相交，一个交点为P，若∠PF1F2=30°，那么椭圆的离心率是（    ）

    A.sin30°                  B.cos30°           C.tan30°                 D.sin45°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆=1(a＞b＞0)与双曲线=1(m＞0,n＞0)有相同的焦点(-c，0)和(c，0)，若c是a、m的等比中项，n2是2m2与c2的等差中项，则椭圆的离心率是(    )

    A.            B.               C.              D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆=1(a＞b＞0)的离心率为，直线y=x+1与椭圆相交于A、B两点，点M在椭圆上， = +，求椭圆的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆=1(a>b>0)与x轴的正半轴交于点A,O是原点.若椭圆上存在一点M,使MA⊥MO,求椭圆离心率e的取值范围.

    查看答案和解析>>

    同步练习册答案