
【题目】如图,已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成二面角的正弦值;
所成二面角的正弦值;
(Ⅲ)若点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(Ⅰ)详见解析(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
(Ⅰ)以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,求得平面
轴建立空间直角坐标系,求得平面![]() 的法向量
的法向量![]() ,利用向量的数量积,求得
,利用向量的数量积,求得![]() ,即可得到
,即可得到![]() 平面
平面![]() .
.
(Ⅱ)由(Ⅰ)求得平面![]() 的一个法向量
的一个法向量![]() ,利用向量的夹角公式,即可求解平面
,利用向量的夹角公式,即可求解平面![]() 与平面
与平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
(Ⅲ)设![]() ,
,![]() ,得
,得![]() ,利用向量的夹角公式,列出方程,求得
,利用向量的夹角公式,列出方程,求得![]() ,得到向量
,得到向量![]() 的坐标,进而求解
的坐标,进而求解![]() 的长.
的长.
(Ⅰ)证明:四边形![]() 为矩形,
为矩形,![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
取![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,如图,
轴建立空间直角坐标系,如图,
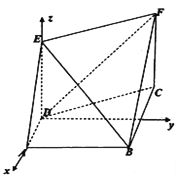
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,∵
,∵![]() ,
,![]() ,
,
由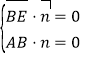 得
得![]() ,不妨设
,不妨设![]() ,
,
又![]() ∴
∴![]() ,∴
,∴![]() ,
,
又∵![]() 平面
平面![]() ∴
∴![]() 平面
平面![]() .
.
(Ⅱ)设平面![]() 的法向量
的法向量![]()
∵![]() ,
,![]() ,
,
由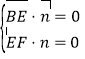 得
得![]() ,不妨设
,不妨设![]() ,
,
∴![]() , ∴
, ∴![]()
∴平面![]() 与平面
与平面![]() 所成二面角的正弦值为
所成二面角的正弦值为![]() .
.
(Ⅲ)∵点![]() 在线段
在线段![]() 上,设
上,设![]() ,
,![]()
∴![]() ,
,
又∵平面![]() 的法向量
的法向量![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]()
∴![]()
![]() ,
,
∴![]() ∴
∴![]() ,
,
∵![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]() ,∴
,∴![]() 的长为
的长为![]() .
.


 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一. 坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村真脱贫,坚持扶贫同扶智相结合,帮助贫困村中60户农民种植苹果、40户农民种植梨、20户农民种植草莓(每户仅扶持种植一种水果),为了更好地了解三种水果的种植与销售情况,现从该村随机选6户农民作为重点考察对象;
(1)用分层抽样的方法,应选取种植苹果多少户?
(2)在上述抽取的6户考察对象中随机选2户,求这2户种植水果恰好相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,
为等差数列,![]() 为等比数列,公比为q(q≠1).令A=
为等比数列,公比为q(q≠1).令A=![]() .A={1,2},
.A={1,2},
(1)当![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,q>0,试比较
,q>0,试比较![]() 与
与![]() (n≥3)的大小?并证明你的结论.
(n≥3)的大小?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() 为自然对数的底数. 设
为自然对数的底数. 设![]() 是
是![]() 的导函数.
的导函数.
(Ⅰ)若![]() 时,函数
时,函数![]() 在
在![]() 处的切线经过点
处的切线经过点![]() ,求
,求![]() 的值;
的值;
(Ⅱ)求函数![]() 在区间
在区间![]() 上的单调区间;
上的单调区间;
(Ⅲ)若![]() ,函数
,函数![]() 在区间
在区间![]() 内有零点,求
内有零点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市收集并整理了该市2019年1月份至10月份各月最低气温与最高气温(单位:℃)的数据,绘制了下面的折线图.( )

已知该城市各月的最低气温与最高气温具有较好的线性关系,则根据折线图,下列结论正确的是
A.最低气温与最高气温为正相关B.10月的最高气温不低于5月的最高气温
C.月温差(最高气温减最低气温)的最大值出现在1月D.最低气温低于0 ℃的月份有4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com