
已知函数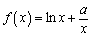 (
(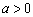 ).
).
(1)求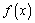 的单调区间;
的单调区间;
⑵如果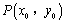 是曲线
是曲线 上的任意一点,若以
上的任意一点,若以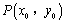 为切点的切线的斜率
为切点的切线的斜率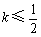 恒成立,求实数
恒成立,求实数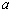 的最小值;
的最小值;
⑶讨论关于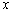 的方程
的方程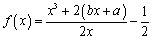 的实根情况.
的实根情况.
科目:高中数学 来源: 题型:
某校高二(6)班学生每周用于数学学习的时间x(单位:小时)与数学成绩y(单位:分)构成如下数据(15,79),(23,97),(16 ,64),(24,92),(12,58).求得的回归直线方程为
,64),(24,92),(12,58).求得的回归直线方程为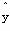 =2.5x+
=2.5x+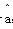 ,则某同学每周学习20小时,估计数学成绩约为多少分?
,则某同学每周学习20小时,估计数学成绩约为多少分?
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列四个结论:
①若命题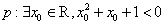 ,则
,则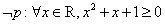 ;
;
②“ ”是“
”是“ ”的充分而不必要条件;
”的充分而不必要条件;
③命题“若 ,则方程
,则方程 有实数根”的逆否命题为:“若方程
有实数根”的逆否命题为:“若方程 没有实数根,则
没有实数根,则 0”;
0”;
④若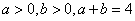 ,则
,则 的最小值为
的最小值为 .
.
其中正确结论的个数为( )




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com