练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某校高二(6)班学生每周用于数学学习的时间x(单位：小时)与数学成绩y(单位：分)构成如下数据(15,79)，(23,97)，(16,64)，(24,92)，(12,58)．求得的回归直线方程为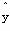＝2.5x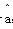＋，则某同学每周学习20小时，估计数学成绩约为多少分？


    解：＝×(15＋23＋16＋24＋12)＝18，

    ＝×(79＋97＋64＋92＋58)＝78.

    把代入＝2.5x＋，

    可求得＝33.

    把x＝20代入＝2.5x＋33得＝2.5×20＋33＝83.

    估计数学成绩约为83分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知的展开式中的系数为32,则b为_________     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知复数（为虚数单位），则．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设有一个回归方程为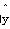＝3－2x，则变量x每增加1个单位时(　　)

        A. 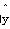平均增加2个单位     B. 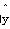平均减少3个单位

    C. 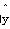平均减少2个单位     D. 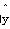平均增加3个单位

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在数列中，，，试猜想出这个数列的通项公式为

                         .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    自变量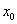变到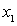 (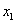>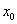)时，函数值的增量与相应自变量的增量之比是函数（   ）

    A． 在区间[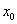,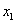]上的平均变化率   B． 在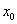处的变化率

    C． 在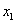处的变化量                D．在区间[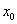,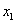]上的导数

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝2－x2－x3的极值情况是                      (　　)

    A．有极大值，没有极小值      B．有极小值，没有极大值

    C．既无极大值也无极小值      D．既有极大值又有极小值

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    要完成下列两项调查：（１）从某社区125户高收入家庭，280户中等收入家庭，95户低收入家庭中选出100户，调查社会购买能力的某项指标；（２）从某中学的15名艺术特长生中选出3名调查学习负担情况．宜采用的抽样方法依次为（　  　）

    A．（１）分层抽样，（２）简单随机抽样       B．（１）简单随机抽样，（２）系统抽样　　

    C．（１）系统抽样，（２）分层抽样　　　     D．（１）（２）都用分层抽样

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数（）．

    (1)求的单调区间；

    ⑵如果是曲线上的任意一点，若以为切点的切线的斜率恒成立，求实数的最小值；

    ⑶讨论关于的方程的实根情况．

    查看答案和解析>>

    同步练习册答案