
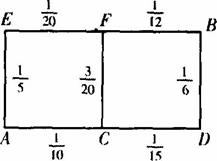
(Ⅰ)请你为他选择一条由A到B的路线,使得途中发生堵车事件的概率最小;
(Ⅱ)若记路线A→C→F→B中遇到堵车的次数为随机变量ξ,求ξ的数学期望.
解:(Ⅰ)记路段MN发生堵车事件为MN,因为各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,所以A→C→D→B路线中遇到堵车的概率为P1,
P1=1-P(![]() )=1-P(
)=1-P(![]() )P(
)P(![]() )P(
)P(![]() )=1-
)=1-![]() ,
,
同理,路线A→C→F→B遇到堵车的概率P2=![]() ,路线A→E→F→B遇到堵车的概率P3=
,路线A→E→F→B遇到堵车的概率P3=![]()
∵P3>P1>P2 因此选择路线A→C→F→B,可使得途中发生堵车事件的概率最小.
(Ⅱ)路线A→C→F→B中遇到的堵车的次数ξ可能为0,1,2,3
P(ξ=0)=P![]()
P(ξ=1)=P![]()
P(ξ=2)=P![]()
P(ξ=3)=P(AC·CF·FB)=![]()
Eξ=0×![]()
答:路线A→C→F→B中遇到的堵车的次数的数学期望是![]()


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
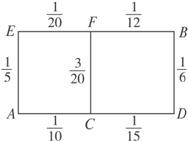
(1)请你为他选择一条由A到B的路段,使得途中发生堵车事件的概率最小;
(2)若记路线A→C→F→B中遇到堵车的次数为随机变量ξ,求ξ的数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
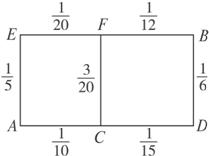
(1)请你为他选择一条由A到B的路段,使得途中发生堵车事件的概率最小;
(2)若该先生上下班行车路线为A→C→F→B和B→F→C→A,分别求他去上班时堵车1次和下班回家堵车2次的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com