
已知椭圆 (a>b>0)经过点M(
(a>b>0)经过点M( ,1),离心率为
,1),离心率为 .
.
(1)求椭圆的标准方程;
(2)已知点P( ,0),若A,B为已知椭圆上两动点,且满足
,0),若A,B为已知椭圆上两动点,且满足 ,试问直线AB是否恒过定点,若恒过定点,请给出证明,并求出该定点的坐标;若不过,请说明理由.
,试问直线AB是否恒过定点,若恒过定点,请给出证明,并求出该定点的坐标;若不过,请说明理由.
(1) 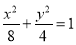 (2) 直线
(2) 直线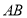 经过定点
经过定点
【解析】
试题分析:(1) 椭圆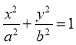 (a>b>0)经过点M(
(a>b>0)经过点M(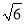 ,1)
,1)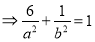 ,
,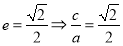
且有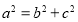 ,通过解方程可得
,通过解方程可得 从而得椭圆的标准方程.
从而得椭圆的标准方程.
(2) 设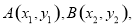 当直线
当直线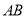 与
与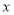 轴不垂直时,设直线的方程为
轴不垂直时,设直线的方程为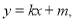
由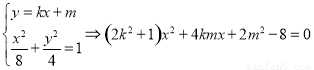
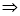
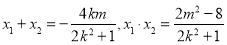
另一方面:
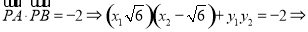
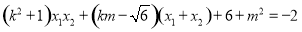
通过以上两式就不难得到关于 的等式,从而探究直线
的等式,从而探究直线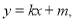 是否过定点;
是否过定点;
至于直线AB斜率不存在的情况,只需对上面的定点进行检验即可.
试题解析:
【解析】
(1)由题意得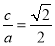 ①
①
因为椭圆经过点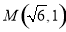 ,所以
,所以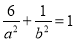 ②
②
又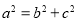 ③
③
由①②③解得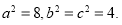
所以椭圆方程为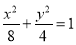 . 4分
. 4分
(2)【解析】
①当直线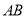 与
与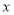 轴不垂直时,设直线的方程为
轴不垂直时,设直线的方程为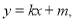
代入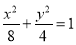 ,消去
,消去 整理得
整理得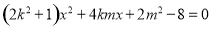 6分
6分
由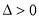 得
得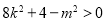 (*)
(*)
设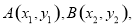 则
则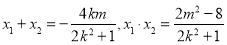
所以,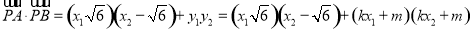
=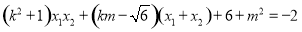 8分
8分
得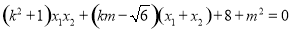
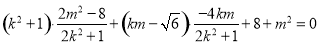
整理得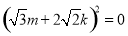
从而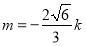 且满足(*)
且满足(*)
所以直线 的方程为
的方程为 10分
10分
故直线 经过定点
经过定点 2分
2分
②当直线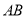 与
与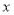 轴垂直时,若直线为
轴垂直时,若直线为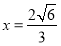 ,此时点
,此时点 、
、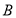 的坐标分别为
的坐标分别为
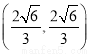 、
、 ,亦有
,亦有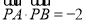 12分
12分
综上,直线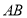 经过定点
经过定点 . 13分
. 13分
考点:1、椭圆的标准方程;2、向量的数量积;3、直线与椭圆的位置关系.


科目:高中数学 来源:2013-2014学年山东省潍坊市高三第二次模拟考试理科数学试卷(解析版) 题型:填空题
现将如图所示的5个小正方形涂上红、黄两种颜色,其中3个涂红色,2个涂黄色,若恰有两个相邻的小正方形涂红色,则不同的涂法种数共有_________.(用数字作答)

查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省淄博市高三复习阶段性诊断考试文科数学试卷(解析版) 题型:选择题
某程序框图如图所示,若输出的S=57,则判断框内填
A. B.
B. C.
C. D.
D.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省济南市高三3月考模拟考试理科数学试卷(解析版) 题型:填空题
已知下列命题:
①设m为直线, 为平面,且m
为平面,且m ,则“m//
,则“m//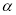 ”是“
”是“ ”的充要条件;
”的充要条件;
②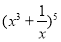 的展开式中含x3的项的系数为60;
的展开式中含x3的项的系数为60;
③设随机变量 ~N(0,1),若P(
~N(0,1),若P(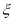 ≥2)=p,则P(-2<
≥2)=p,则P(-2< <0)=
<0)= ;
;
④若不等式|x+3|+|x-2|≥2m+1恒成立,则m的取值范围是(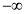 ,2);
,2);
⑤已知奇函数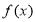 满足
满足 ,且0<x<
,且0<x< 时
时 ,则函数
,则函数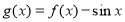 在[
在[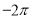 ,
,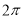 ]上有5个零点.
]上有5个零点.
其中真命题的序号是 (写出全部真命题的序号).
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省济南市高三3月考模拟考试理科数学试卷(解析版) 题型:选择题
已知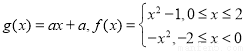 ,对
,对 ,使
,使 成立,则a的取值范围是( )
成立,则a的取值范围是( )
(A)[-1,+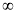 ) (B)[-1,1] (C)(0,1] (D)(-
) (B)[-1,1] (C)(0,1] (D)(-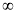 ,l]
,l]
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省济南市高三3月考模拟考试文科数学试卷(解析版) 题型:填空题
如图,长方体ABCD—A1B1C1D1,有一动点在此长方体内随机运动,则此动点在三棱锥A—A1BD内的概率为 .

查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省日照市高三5月统一质量检测考试文科数学试卷(解析版) 题型:填空题
已知变量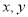 满足约束条件
满足约束条件 的最大值为5,且k为负整数,则k=____________.
的最大值为5,且k为负整数,则k=____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com