Question

【题目】如图，AB是圆O的直径，G是AB延长线上的一点，GCD是圆O的割线，过点G作AG的垂线，交直线AC于点E，交直线 AD于点F，过点G作圆O的切线，切点为H．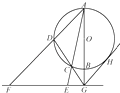
（1）求证：C，D，E，F四点共圆；
（2）若GH=8，GE=4，求EF的长．

Answer 1

【答案】
（1）解：连接DB，

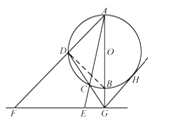
∵AB是⊙O的直径，∴∠ADB=90°，

在Rt△ABD和Rt△AFG中，∠ABD=∠AFE，

又∵∠ABD=∠ACD，∠ACD=∠AFE．

∴C，D，E，F四点共圆；

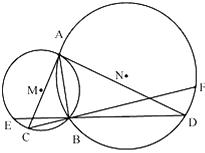
（2）解：∵C，D，E，F四点共圆，∴GEGF=GCGD．

∵GH是⊙O的切线，∴GH2=GCGD，∴GH2=GEGF．

又因为GH=8，GE=4，所以GF=16．

∴EF=GF﹣GE=12．

【解析】（1）连接DB，利用AB是⊙O的直径，可得∠ADB=90°，在Rt△ABD和Rt△AFG中，∠ABD=∠AFE，又同弧所对的圆周角相等可得∠ACD=∠ABD，进而得到∠ACD=∠AFE即可证明四点共圆；（2）由C，D，E，F四点共圆，利用共线定理可得GEGF=GCGD．由GH是⊙O的切线，利用切割线定理可得GH2=GCGD，进而得到GH2=GEGF即可．