Question

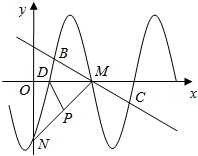
2．函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|≤$\frac{π}{2}$）的部分图象如图所示．其中L，M，N分别是函数f（x）的图象与坐标轴的交点．且LM=3OL，∠NM0=45°，线段MN的中点P的坐际为（2，一2）．
（1）求函数f（x）的解析式；
（2）求函数f（x）的单凋递减区间以及当x∈[4，8]时，函数f（x）的取值范围．
（3）若过点M的直线与函数f（x）的图象交于B，C两点．求（$\overrightarrow{LB}+\overrightarrow{LC}$）•（$\overrightarrow{LC}-\overrightarrow{MC}$）的值．

Answer 1

分析 （1）由题意可得M，N的坐标，利用距离公式求出周期，ω的值，通过五点法求出函数的解析式，即可求出φ，A的值，即可求得函数解析式．
（2）由2kπ+$\frac{π}{2}$≤$\frac{π}{3}$x-$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$，k∈Z可解得f（x）的单凋递减区间，当x∈[4，8]时，$\frac{π}{3}$x-$\frac{π}{3}$∈[π，$\frac{7π}{3}$]，可得sin（$\frac{π}{3}$x-$\frac{π}{3}$）∈[-1，$\frac{\sqrt{3}}{2}$]，即可得解．
（3）利用向量的基本运算和向量的数量积定义即可得到结论．

解答 解：（1）∵函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|≤$\frac{π}{2}$）与坐标轴的三个交点L，M，N满足LM=3OL，∠NMO=$\frac{π}{4}$，P（2，-2）为线段MN的中点，
∴可得M（4，0），N（0，-4），|LM|=3，T=6=$\frac{2π}{ω}$，解得ω=$\frac{π}{3}$，
∴函数经过M，N，有$\left\{\begin{array}{l}{Asin（\frac{π}{3}×4+φ）=0}\\{-4=Asin（\frac{π}{3}×0+φ）}\end{array}\right.$，
∵|φ|≤$\frac{π}{2}$，
∴φ=-$\frac{π}{3}$，
∴解得A=$\frac{8\sqrt{3}}{3}$．
∴函数f（x）的解析式为：f（x）=$\frac{8\sqrt{3}}{3}$sin（$\frac{π}{3}$x-$\frac{π}{3}$）．
（2）由2kπ+$\frac{π}{2}$≤$\frac{π}{3}$x-$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$，k∈Z可解得f（x）的单凋递减区间为：[6k+$\frac{5}{2}$，6k+$\frac{11}{2}$]，k∈Z．
∵当x∈[4，8]时，$\frac{π}{3}$x-$\frac{π}{3}$∈[π，$\frac{7π}{3}$]，可得sin（$\frac{π}{3}$x-$\frac{π}{3}$）∈[-1，$\frac{\sqrt{3}}{2}$]，
∴f（x）=$\frac{8\sqrt{3}}{3}$sin（$\frac{π}{3}$x-$\frac{π}{3}$）∈[-$\frac{8\sqrt{3}}{3}$，4]．
（3）∵由题意及向量的平行四边形法则可知：$\overrightarrow{LB}+\overrightarrow{LC}$=2$\overrightarrow{LM}$，又$\overrightarrow{LC}-\overrightarrow{MC}$=$\overrightarrow{LC}-（-\overrightarrow{CM}）$=$\overrightarrow{LC}+\overrightarrow{CM}=\overrightarrow{LM}$，
∴（$\overrightarrow{LB}+\overrightarrow{LC}$）•（$\overrightarrow{LC}-\overrightarrow{MC}$）=2$\overrightarrow{LM}$$•\overrightarrow{LM}$=2|$\overrightarrow{LM}$|²=2×3²=18．

点评 本题考查三角函数的解析式的求法，正弦函数的图象和性质，考查了向量的数量积运算，利用三角函数的图象和性质是解决本题的关键．属于基本知识的考查．