
����Ŀ��2016����˫�����ڼ䣬���ٹ�·�����϶࣮ij���鹫˾��һ����������������С�������а������������Ⱥ�ÿ���50���ͳ�ȡһ���ij���������ȡ40����ʻԱ����ѯ�ʵ��飬��������ij�θ��ٹ�·�ij���![]() �ֳ����Σ�
�ֳ����Σ� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
��õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
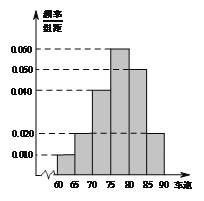
��I��ij���鹫˾�ڲ����У��õ�����ʲô����������
��II������40��С�ͳ������ٵ���������λ����ƽ�����Ĺ���ֵ��
(III)���ӳ�����![]() �ij������γ�ȡ2����������
�ij������γ�ȡ2����������![]() �ij���������һ���ĸ��ʣ�
�ij���������һ���ĸ��ʣ�
���𰸡�(1) ϵͳ������(2)77.5,77.5,77(3) ![]()
�������������������1�����ݳ���Ϊ�Ⱦ������֪��ϵͳ��������2����Ƶ�ʷֲ�ֱ��ͼ������Ϊ��ߵľ��ε��е�ĺ����꣬��λ����ߺ��ұߵ�ֱ��ͼ�������ȣ��ɴ˿��Թ�����λ��ֵ��ƽ�����Ĺ���ֵ����ÿ��С���ε�������Ծ��εױ��е������֮�ͣ���3��������֪������![]() �ij�����6���оٷ��õ��γ�ȡ2�������н������Ϲŵ��������⡣
�ij�����6���оٷ��õ��γ�ȡ2�������н������Ϲŵ��������⡣
���������
��1��ϵͳ������
��2�������Ĺ���ֵΪ��ߵľ��ε��е㣬��![]()
��ͼ����������Ӧ�ij���Ϊ![]() ������λ���Ĺ���ֵΪ��
������λ���Ĺ���ֵΪ��
![]() �����
�����![]()
����λ���Ĺ���ֵΪ![]() ��
��
ƽ�����Ĺ���ֵΪ��
![]()
��3��������![]() �ij�������2
�ij�������2
������![]() �ij�������4
�ij�������4
�賵����![]() �ij���Ϊ
�ij���Ϊ![]() ��������
��������![]() �ij���Ϊ
�ij���Ϊ![]() ��������¼��У�
��������¼��У�
![]()
��15�֣�
���У�������![]() �ij���������һ�����¼��У�
�ij���������һ�����¼��У�
![]()
��14��
���Գ�����![]() �ij���������һ���ĸ���Ϊ
�ij���������һ���ĸ���Ϊ![]() .
.


 ������״Ԫ��ҵϵ�д�
������״Ԫ��ҵϵ�д� ��ʱ�ƿ�������ϰϵ�д�
��ʱ�ƿ�������ϰϵ�д� һ��һ��һ��ͨϵ�д�
һ��һ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ������
������![]() ��
�� ![]() �ڵ�
�ڵ�![]() �������߽�
�������߽�![]() ���ڵ�
���ڵ�![]() ��ֱ��
��ֱ��![]() ������
������![]() �Ҵ�ֱ��
�Ҵ�ֱ��![]() �ᣮ
�ᣮ
��1�����߶�![]() �ij���
�ij���
��2���費������![]() ��
��![]() �Ķ�ֱ��
�Ķ�ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ����ֱ��
����ֱ��![]() ��
��![]() ��
��![]() ��б�����γɵȲ����У����ʣ�
��б�����γɵȲ����У����ʣ� ![]() �Ƿ�����㣿��˵�����ɣ�
�Ƿ�����㣿��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{an}����an+1+����1��nan=2n��1����{an}��ǰ60���Ϊ�� ��
A. 3690 B. 3660 C. 1845 D. 1830
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ ![]() �Ķ������ǣ� ��
�Ķ������ǣ� ��
A.{x|x����4��x��3}
B.{x|��4��x��3}
C.{x|x�ܩ�4��x��3}
D.{x|��4��x��3}
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�IJ���ʽax2+��1��a��x��1��0
��1����a=2ʱ����ʽ�Ľ⼯��
��2����a����1ʱ����ʽ�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������12������ͼ��ij�н���1�·�ǰ30���������ָ����AQI��������ͼ.

��1�����ݸ�ͼ�����ڴ���������Ƶ�ʷֲ���������ͼ�в�ȫ��Щ���ݵ�Ƶ�ʷֲ�ֱ��ͼ��
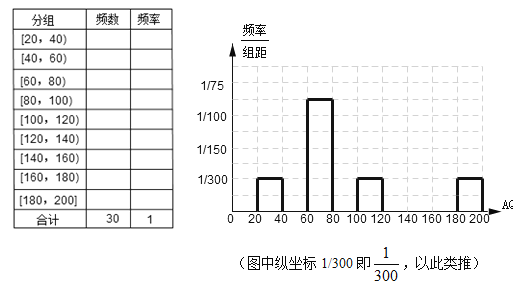
��2������������ָ����AQI��С��100ʱ����ʾ��������������ij�����ѡ����������30�����ijһ��
������У�����������Ϣ���ܷ���Ϊ���˵��ﵱ��������������Ŀ����Գ���60%��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĸ�����
���������ӳ����������������������ƽ��ֵ��ƫ��̶ȣ�
���Ӻ���2008������������г�ȡһ������Ϊ100������,�ֲ���ϵͳ��������Ӧ����8��,��ÿ�����屻�鵽�ĸ��ʾ�Ϊ![]() ��
��
���������г�ȡ���������ݹ���m��a��n��b��p��c���������ƽ����![]() �Ĺ���ֵΪ
�Ĺ���ֵΪ![]() ��
��
��ij��ѧ����ϵͳ�����������Ӹ�У��һ�꼶ȫ��800��ѧ���г�50��ѧ�������ݽ�����飬�ֽ�800��ѧ����001��800���б�ţ���֪��497--512��16������ȡ�õ�ѧ�������503�����ʼ�ڵ�1С��00l��016������鵽��ѧ�������007��
����������ĸ����� _____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �붨��
�붨��![]() �ľ����������ֱ��
�ľ����������ֱ��![]() �ľ���ı���
�ľ���ı���![]() ��
��![]() ���ǵ�
���ǵ�![]() �Ĺ켣Ϊ
�Ĺ켣Ϊ![]() .
.
��1��������![]() �ķ��̣�
�ķ��̣�
��2�����ڶ���![]() ��������
��������![]() ��ֱ��
��ֱ��![]() ������
������![]() ���ڲ�ͬ������
���ڲ�ͬ������![]() ��
��![]() ������
������![]() ������Բ�뾶�����ֵ.
������Բ�뾶�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڲ�������ˮ��Ⱦ���أ�Ϊ�˻�õ�һ�ֵ�ˮ�����ϣ�DZˮԱ��ҪDZ��ˮ��Ϊ60��ˮ������ҵ�����ݾ��飬DZˮԱ��DZ��ƽ���ٶ�Ϊ![]() ����/��λʱ�䣩��ÿ��λʱ����������
����/��λʱ�䣩��ÿ��λʱ����������![]() ����������ˮ����ҵ10����λʱ�䣬ÿ��λʱ����������
����������ˮ����ҵ10����λʱ�䣬ÿ��λʱ����������![]() ������������ˮ���ƽ���ٶ�Ϊ
������������ˮ���ƽ���ٶ�Ϊ![]() ����/��λʱ�䣩��ÿ��λʱ����������
����/��λʱ�䣩��ÿ��λʱ����������![]() ���������Ǹ�DZˮԱ��ɴ˴������������������Ϊ
���������Ǹ�DZˮԱ��ɴ˴������������������Ϊ![]() ������.
������.
��1����![]() ����
����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2����![]() ������DZ�ٶ�
������DZ�ٶ�![]() ȡʲôֵʱ��������������������.
ȡʲôֵʱ��������������������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com