△ABC中角A，B，C的对应边分别为a，b，c，满足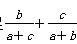
≥1，则角A的范围是( )
科目：高中数学 来源： 题型：
已知集合A＝{x êx2＋(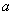
－1)x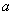－＞0}，B＝{x ê(x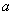＋)(x＋b)＞0}，其中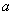≠b，M＝{x êx2－2x－3≤0}，全集I＝R．
(1)若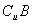
＝M，求a、b的值；
(2)若a＞b＞－1，求A∩B；
(3)若a2＋
∈
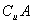，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知向量a＝(sin x,2cos x)，b＝(2sin x，sin x)，设函数f(x)＝a·b.
(1)求f(x)的单调递增区间；
(2)若将f(x)的图象向左平移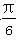
个单位，得到函数g(x)的图象，求函数g(x)在区间
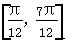上的最大值和最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
在△ABC中，角A，B，C所对的边分别为a，b，c，S表示△ABC的面积，若acos B＋bcos A＝csin C，S＝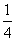
(b2＋c2－a2)，则角B等于( )
A．90° B．60°
C．45° D．30°
查看答案和解析>>
科目：高中数学 来源： 题型：
已知数列{an}是等差数列，{bn}是等比数列，其中a1＝b1＝1，a2≠b2，且b2为a1，a2的等差中项，a2为b2，b3的等差中项．
(1)求数列{an}与{bn}的通项公式；
(2)记cn＝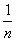
(a1＋a2＋…＋an)(b1＋b2＋…＋bn)，求数列{cn}的前n项和Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
≥1，得b(a＋b)＋c(a＋c)≥(a＋c)(a＋b)，化简得b2＋c2－a2≥bc，即
≥
，即cos A≥
，故选A.
与
均为纯虚数，则
。
的最大值为________．