
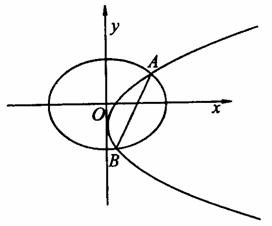
(Ⅰ)当AB⊥x轴时,求m、p的值,并判断抛物线C2的焦点是否在直线AB上;
(Ⅱ)是否存在m、p的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的m、p的值;若不存在,请说明理由.
21.解 (Ⅰ)当AB⊥x轴时,点A、B关于x轴对称,所以m=0,直线AB的方程为x=1,从而点A的坐标为(1,![]() )或(1,-
)或(1,-![]() ).
).
因为点A在抛物线上,所以![]() =2p,即p=
=2p,即p=![]() .此时C2的焦点坐标为(
.此时C2的焦点坐标为(![]() ,0),该焦点不在直线AB上.
,0),该焦点不在直线AB上.
(Ⅱ)解法一 假设存在m、p的值使C2的焦点恰在直线AB上,由(Ⅰ)知直线AB的斜率存在,故可设直线AB的方程为y=k(x-1).
由 消去y得(3+4k2)x2-8k2x+4k2-12=0. ……①
消去y得(3+4k2)x2-8k2x+4k2-12=0. ……①
设A、B的坐标分别为(x1,y1)、(x2,y2),则x1、x2是方程①的两根,x1+x2=![]() .
.
由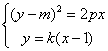 消去y得
消去y得
(kx-k-m)2=2px. ……②
因为C2的焦点F′(![]() ,m)在y=k(x-1)上,
,m)在y=k(x-1)上,
所以m=k(![]() -1),即m+k=
-1),即m+k=![]() .代入②有(kx-
.代入②有(kx-![]() )2=2px.
)2=2px.
即k2x2-p(k2+2)x+![]() =0. ……③
=0. ……③
由于x1、x2也是方程③的两根,所以x1+x2=![]() .
.
从而![]() . ……④
. ……④
又AB过C1、C2的焦点,
所以|AB|=(x1+![]() )+(x2+
)+(x2+![]() )=x1+x2+p=(2-
)=x1+x2+p=(2-![]() x1)+(2-
x1)+(2-![]() ),
),
则p=4-![]() (x1+x2)=4-
(x1+x2)=4-![]() =
=![]() . ……⑤
. ……⑤
由④、⑤得![]() =
=![]() .
.
即k4-5k2-6=0.解得k2=6.
于是k=±![]() ,p=
,p=![]() .
.
因为C2的焦点F′(![]() ,m)在直线y=±
,m)在直线y=±![]() (x-1)上,所以m=±
(x-1)上,所以m=±![]() (
(![]() -1).
-1).
即m=![]() 或m=-
或m=-![]() .
.
由上知,满足条件的m、p存在,且m=![]() 或m=-
或m=-![]() ,p=
,p=![]() .
.
解法二 设A、B的坐标分别为(x1,y1)、(x2,y2),
因为AB即过C1的右焦点F(1,0),又过C2的焦点F′(![]() ,m),
,m),
所以|AB|=(x1+![]() )+(x2+
)+(x2+![]() )=x1+x2+p=(2-
)=x1+x2+p=(2-![]() x1)+(2-
x1)+(2-![]() x2).
x2).
即x1+x2=![]() (4-p). ……①
(4-p). ……①
由(Ⅰ)知x1≠x2,p≠2,于是直线AB的斜率k= ,
,
且直线AB的方程是y=![]() (x-1). ……②
(x-1). ……②
所以y1+y2=![]() (x1+x2-2)=
(x1+x2-2)=![]() . ……③
. ……③
又因为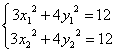 ,所以3(x1+x2)+4(y1+y2)·
,所以3(x1+x2)+4(y1+y2)·![]() =0. ……④
=0. ……④
将①、②、③代入④得m2= . ……⑤
. ……⑤
因为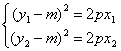 ,所以y1+y2-2m=2p
,所以y1+y2-2m=2p![]() ……⑥
……⑥
将②、③代入⑥得m2=![]() . ……⑦
. ……⑦
由⑤、⑦得![]() =
=![]() .即3p2+20p-32=0.
.即3p2+20p-32=0.
解得p=![]() 或p=-8(舍去).
或p=-8(舍去).
将p=![]() 代入⑤得m2=
代入⑤得m2=![]() ,所以m=
,所以m=![]() 或m=-
或m=-![]() .
.
由上知,满足条件的m、p存在,且m=![]() 或m=-
或m=-![]() ,p=
,p=![]() .
.


科目:高中数学 来源: 题型:
A.8 B.12 C.9 D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
A.2 B.4 C.8 D.16
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练24练习卷(解析版) 题型:解答题
已知椭圆C1: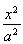 +
+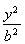 =1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
=1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
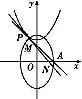
(1)求椭圆C1的方程;
(2)设点P在抛物线C2:y=x2+h(h∈R)上,C2在点P处的切线与C1交于点M,N.当线段AP的中点与MN的中点的横坐标相等时,求h的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练24练习卷(解析版) 题型:解答题
在平面直角坐标系xOy中,已知椭圆C1: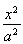 +
+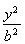 =1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
=1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
(1)求椭圆C1的方程;
(2)设直线l同时与椭圆C1和抛物线C2:y2=4x相切,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练24练习卷(解析版) 题型:选择题
已知椭圆C1: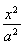 +
+ =1(a>b>0)与双曲线C2:x2-
=1(a>b>0)与双曲线C2:x2-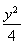 =1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
=1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
(A)a2= (B)a2=13
(B)a2=13
(C)b2= (D)b2=2
(D)b2=2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com