
我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”.已知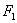 、
、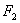 是一对相关曲线的焦点,
是一对相关曲线的焦点,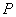 是它们在第一象限的交点,当
是它们在第一象限的交点,当 时,这一对相关曲线中双曲线的离心率是( )
时,这一对相关曲线中双曲线的离心率是( )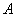 .
.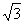
 .
.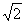
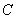 .
.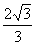
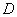 .
.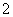
A
解析试题分析:设F1P=m,F2P=n,F1F2=2c,由余弦定理4c2=m2+n2-mn,设a1是椭圆的长半轴,a1是双曲线的实半轴,由椭圆及双曲线定义,得m+n=2a1,m-n=2a1,由此能求出结果.解:设F1P=m,F2P=n,F1F2=2c,由余弦定理得(2c)2=m2+n2-2mncos60°,即4c2=m2+n2-mn,设a1是椭圆的长半轴,a1是双曲线的实半轴,由椭圆及双曲线定义,得m+n=2a1,m-n=2a1,∴m=a1+a2,n=a1-a2,将它们及离心率互为倒数关系代入前式得a12-4a1a2+a12=0, a1=3a2,e1•e2= 解得e2=
解得e2=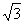 .故选A.
.故选A.
考点:双曲线和椭圆的简单性质
点评:本题考查双曲线和椭圆的简单性质,解题时要认真审题,注意正确理解“相关曲线”的概念.


科目:高中数学 来源: 题型:单选题
如图,有一条长度为1的线段EF,其端点E、F分别在边长为3的正方形ABCD的四边上滑动,当F沿正方形的四边滑动一周时,EF的中点M所形成的轨迹长度最接近于( )
| A.8 | B.11 |
| C.12 | D.10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com