
经过点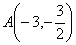 ,倾斜角为
,倾斜角为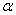 的直线
的直线 ,与曲线
,与曲线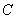 :
: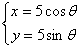 (
(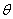 为参数)相交于
为参数)相交于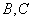 两点.
两点.
(1)写出直线 的参数方程,并求当
的参数方程,并求当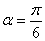 时弦
时弦 的长;
的长;
(2)当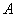 恰为
恰为 的中点时,求直线
的中点时,求直线 的方程;
的方程;
(3)当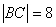 时,求直线
时,求直线 的方程;
的方程;
(4)当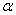 变化时,求弦
变化时,求弦 的中点的轨迹方程.
的中点的轨迹方程.
(1)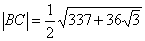 ;(2)
;(2) ;(3)
;(3) 或
或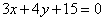
(4)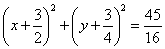
【解析】
试题分析:(1)将参数方程转化为直角坐标系下的普通方程;掌握常见的将参数方程转化为直角坐标系下的普通方程;(2)解决直线和曲线的综合问题:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与曲线的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式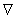 :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.(4)根据题意设点根据点到直线的距离公式.
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.(4)根据题意设点根据点到直线的距离公式.
试题解析:解:(1) 的参数方程
的参数方程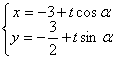 (
(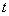 为参数). 1分
为参数). 1分
曲线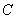 化为:
化为: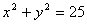 ,将直线参数方程的
,将直线参数方程的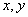 代入,得
代入,得
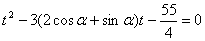
∵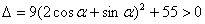 恒成立, 3分
恒成立, 3分
∴方程必有相异两实根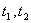 ,且
,且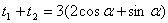 ,
,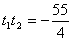 .
.
∴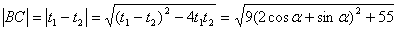
∴当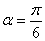 时,
时,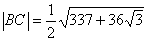 . 5分
. 5分
(2)由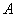 为
为 中点,可知
中点,可知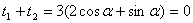 ,
,
∴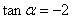 ,
,
故直线 的方程为
的方程为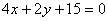 . 7分
. 7分
(3)∵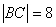 ,得
,得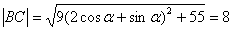
∴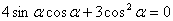 ,
,
∴ 或
或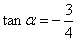
故直线 的方程为
的方程为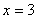 或
或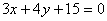 9分
9分
(4)∵ 中点对应参数
中点对应参数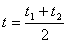
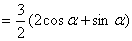
∴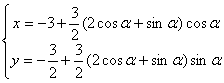 ( 参数
( 参数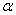
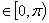 ),消去
),消去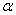 ,得
,得
弦 的中点的轨迹方程为
的中点的轨迹方程为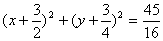 ;
;
轨迹是以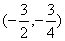 为圆心,
为圆心,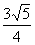 为半径的圆. 10分
为半径的圆. 10分
考点:(1)求弦长问题;(2)求直线方程;(3)中点弦的轨迹方程.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
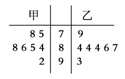 青年歌手大奖赛共有10名选手参赛,并请了7名评委.如图所示的茎叶图是7名评委给参加最后决赛的两位选手甲、乙评定的成绩,去掉一个最高分和一个最低分后,甲、乙选手剩余数据的平均成绩分别为________、________.
青年歌手大奖赛共有10名选手参赛,并请了7名评委.如图所示的茎叶图是7名评委给参加最后决赛的两位选手甲、乙评定的成绩,去掉一个最高分和一个最低分后,甲、乙选手剩余数据的平均成绩分别为________、________.
查看答案和解析>>
科目:高中数学 来源: 题型:
函数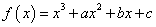 ,在定义域
,在定义域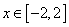 上表示的曲线过原点,且在
上表示的曲线过原点,且在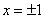 处的切线斜率均为
处的切线斜率均为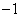 .有以下命题:
.有以下命题:
①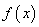 是奇函数;②若
是奇函数;②若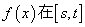 内递减,则
内递减,则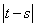 的最大值为4;③
的最大值为4;③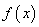 的最大值为M,最小值为m,则
的最大值为M,最小值为m,则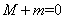 ;④若对
;④若对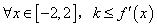 恒成立,则
恒成立,则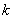 的最大值为2.其中正确命题的个数为 ( )
的最大值为2.其中正确命题的个数为 ( )
A. 1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
某种彩票的抽奖是从写在36个球上的36个号码中随机摇出7个.有人统计了过去中特等奖的号码,声称某一号码在历次特等奖中出现的次数最多,它是一个幸运号码,人们应该买这一号码;也有人说,若一个号码在历次特等奖中出现的次数最少,由于每个号码出现的机会相等,应该买这一号码,你认为他们的说法对吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com