
【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运
会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.
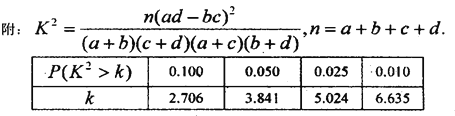
【答案】(1)见解析;(2)能在犯错误的概率不超过5﹪的前提下认为不同年龄与支持申办奥运无关;(3)![]() .
.
【解析】试题分析:(1)根据条件中所给的数据填上对应的数据,即可得到列联表;(2 )假设聋哑没有关系,根据上一问做出的列联表,把求得的数据代入求观测值的公式求出观测值,把观测值同临界值进行比较得到结论;(3 ) 利用列举法,确定基本事件的个数,即利用古典概型概率公式可求出 的概率..
试题解析:
支 持 | 不 支 持 | 总 计 | |
年龄不大于50岁 | 20 | 60 | 80 |
年龄大于50岁 | 10 | 10 | 20 |
合 计 | 30 | 70 | 100 |
(1)
(2)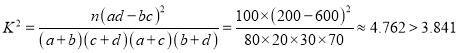
所以能在犯错误的概率不超过5﹪的前提下认为不同年龄与支持申办奥运无关.
(3)记5人为a b c d e,其中a b表示教师,从5人任意抽3人的所有等可能事件是:
abc,abd,abe,acd,ace,ade,bcd,bce,bde,cde共10个,其中至多一位教师有7个基本事件:acd,ace,ade,bcd,bce,bde,cde,所以所求概率是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】端午节吃粽子是我国的传统习俗.设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同.从中任意选取3个.
(1)求三种粽子各取到1个的概率;
(2)设X表示取到的豆沙粽个数,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(1)求![]() 到平面
到平面![]() 的距离
的距离
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4;坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标中,曲线
轴正半轴为极轴的极坐标中,曲线![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程.
的直角坐标方程.
(Ⅱ)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方形ABCD中,AB=3,AD=4.现将长方形沿对角线BD折起,使AC=a,得到一个四面体A-BCD,如图所示.
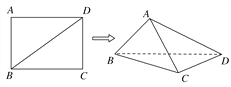
(1)试问:在折叠的过程中,直线AB与CD能否垂直?若能,求出相应a的值;若不能,请说明理由;
(2)求四面体A-BCD体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两袋中各装有大小相同的小球9个,其中甲袋中红色、黑色、白色小球的个数分别为2,3,4,乙袋中红色、黑色、白色小球的个数均为3,某人用左右手分别从甲、乙两袋中取球.
(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(2)若左右手依次各取两球,称同一手中两球颜色相同的取法为成功取法,记两次取球(左右手依次各取两球为两次取球)的成功取法次数为随机变量X,求X的分布列。
查看答案和解析>>
科目:高中数学 来源: 题型:
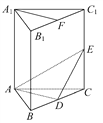
【题目】如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.
求证:(1)平面ADE⊥平面BCC1B1.
(2)直线A1F∥平面ADE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com