【题目】
是指空气中直径小于或等于2.5微米的颗粒物（也称可入肺颗粒物），为了探究车流量与的浓度是否相关，现采集到某城市周一至周五某时间段车流量与浓度的数据如下表：
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 39 | 40 | 42 | 44 | 45 |
（1）根据上表数据，求出这五组数据组成的散点图的样本中心坐标；
（2）用最小二乘法求出
关于
的线性回归方程
；
（3）若周六同一时间段车流量是100万辆，试根据（2）求出的线性回归方程预测，此时的浓度是多少？
（参考公式：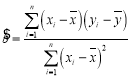
，
）
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
极坐标系的极点为直角坐标系
的原点，极轴为
轴的正半轴，两种坐标系中的长度单位相同，已知曲线
的极坐标方程为
.
（1）求
的直角坐标方程；
（2）直线
（
为参数）与曲线
交于
两点，与
轴交于
，求
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某精准扶贫帮扶单位，为帮助定点扶贫村真正脱贫，坚持扶贫同扶智相结合，帮助精准扶贫户利用互联网电商渠道销售当地特产苹果.苹果单果直径不同单价不同，为了更好的销售，现从该精准扶贫户种植的苹果树上随机摘下了50个苹果测量其直径，经统计，其单果直径分布在区间[50，95]内（单位：
），统计的茎叶图如图所示：
（Ⅰ）从单果直径落在[72，80）的苹果中随机抽取3个，求这3个苹果单果直径均小于76的概率；
（Ⅱ）以此茎叶图中单果直径出现的频率代表概率.直径位于[65，90）内的苹果称为优质苹果，对于该精准扶贫户的这批苹果，某电商提出两种收购方案：
方案
：所有苹果均以5元/千克收购；
方案
：从这批苹果中随机抽取3个苹果，若都是优质苹果，则按6元/干克收购；若有1个非优质苹果，则按5元/千克收购；若有2个非优质苹果，则按4.5元/千克收购；若有3个非优质苹果，则按4元/千克收购.
请你通过计算为该精准扶贫户推荐收益最好的方案.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知梯形
中，
，
，
，四边形
为矩形，
，平面
平面．
（Ⅰ）求证：
平面
；
（Ⅱ）求平面与平面
所成锐二面角的余弦值；
（Ⅲ）在线段
上是否存在点
，使得直线
与平面所成角的正弦值为
，若存在，求出线段的长；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】我国古代数学名著《九章算术商功》中阐述：“斜解立方，得两堑堵．斜解堑堵，其一为阳马，一为鳖臑．阳马居二，鳖臑居一，不易之率也．合两鳖臑三而一，验之以棊，其形露矣．”若称为“阳马”的某几何体的三视图如图所示，图中网格纸上小正方形的边长为1，对该几何体有如下描述：
①四个侧面都是直角三角形；
②最长的侧棱长为
；
③四个侧面中有三个侧面是全等的直角三角形；
④外接球的表面积为24π．
其中正确的描述为____．
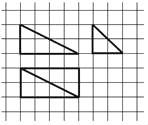
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设抛物线
：
的焦点为
，直线
与交于
，
两点，
的面积为
.
（1）求的方程；
（2）若
，
是上的两个动点，
，试问：是否存在定点
，使得
？若存在，求的坐标，若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在
内,发布成绩使用等级制各等级划分标准见下表,规定： 
、
、
三级为合格等级, 
为不合格等级.
百分制 |
|
|
|
|
等级 |
|
|
|
|
为了解该校高一年级学生身体素质情况,从中抽取了
名学生的原始成绩作为样本进行统计,按照
的分组作出频率分布直方图如图
所示,样本中分数在
分及以上的所有数据的茎叶图如图
所示.
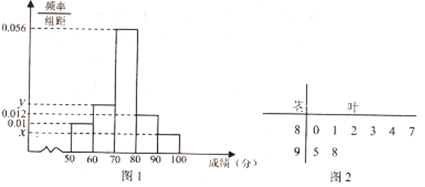
（1）求
和频率分布直方图中的
的值；
（2）根据样本估计总体的思想，以事件发生的频率作为相应事件发生的概率，若在该校高一学生任选
人,求至少有
人成绩是合格等级的概率；
（3）在选取的样本中,从
、
两个等级的学生中随机抽取了
名学生进行调研,记
表示所抽取的
名学生中为
等级的学生人数,求随机变量
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
