
【题目】设![]() 为自然数1、2、3、4的一个全排列,且满足
为自然数1、2、3、4的一个全排列,且满足![]() ,则这样的排列有_______个.
,则这样的排列有_______个.
【答案】9
【解析】
利用和值为6,分解为4个非负数的和,最大值为3,最小值为0,列出所有情况即可.
x1、x2、x3、x4为自然数1、2、3、4的一个全排列,且满足|x1﹣1|+|x2﹣2|+|x3﹣3|+|x4﹣4|=6,
可得4个数的和为6,共有,0+0+3+3=6;1+1+1+3=6;0+1+2+3=6;1+1+2+2=6;
所有x1、x2、x3、x4分别为:
0+0+3+3=6;类型有:
4,2,3,1;
1+1+1+3=6;类型有:
2,3,4,1;
4,1,2,3;
0+1+2+3=6;类型有:
4,1,3,2;
4,2,1,3;
3,2,4,1;
2,4,3,1;
1+1+2+2=6;类型有:
2,4,1,3;
3,1,4,2;
共9种.
故答案为:9.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】设甲、乙、丙三个羽毛球协会的运动员人数分别为18,9,18,先采用分层抽样的方法从这三个协会中抽取5名运动员参加比赛.
(1)求应从这三个协会中分别抽取的运动员人数;
(2)将抽取的5名运动员进行编号,编号分别为![]() ,从这5名运动员中随机抽取2名参加双打比赛. 设“编号为
,从这5名运动员中随机抽取2名参加双打比赛. 设“编号为![]() 的两名运动员至少有一人被抽到” 为事件A,求事件A发生的概率.
的两名运动员至少有一人被抽到” 为事件A,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,内接于圆![]() 的正方形
的正方形![]() 边长为1,圆
边长为1,圆![]() 内切于正方形
内切于正方形![]() ,正方形
,正方形![]() 内接于圆
内接于圆![]() ,···,正方形
,···,正方形![]() 内接于圆
内接于圆![]() ,圆
,圆![]() 内切于正方形
内切于正方形![]() ,正方形
,正方形![]() 内接于圆
内接于圆![]() ,由此无穷个步骤进行下去记圆
,由此无穷个步骤进行下去记圆![]() 的面积记作
的面积记作![]() ,记正方形
,记正方形![]() 的面积记作
的面积记作![]() .
.
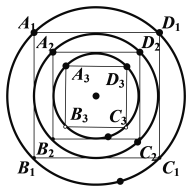
(1)求![]() 的值
的值
(2)记![]() 的所有项和为
的所有项和为![]() ,
,![]() 的所有项和为
的所有项和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有甲,乙两个车间生产同一种产品,,甲车间有工人![]() 人,乙车间有工人
人,乙车间有工人![]() 人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:
人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:![]() )进行统计,按照
)进行统计,按照![]() 进行分组,得到下列统计图.
进行分组,得到下列统计图.
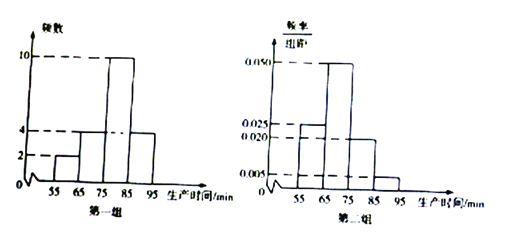
![]() 分别估算两个车间工人中,生产一件产品时间少于
分别估算两个车间工人中,生产一件产品时间少于![]() 的人数
的人数
![]() 分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
![]() 从第一组生产时间少于
从第一组生产时间少于![]() 的工人中随机抽取
的工人中随机抽取![]() 人,记抽取的生产时间少于
人,记抽取的生产时间少于![]() 的工人人数为随机变量
的工人人数为随机变量![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】社区服务是高中学生社会实践活动的一个重要内容,汉中某中学随机抽取了100名男生、100名女生,了解他们一年参加社区服务的时间,按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:小时)进行统计,得出男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.
(单位:小时)进行统计,得出男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.
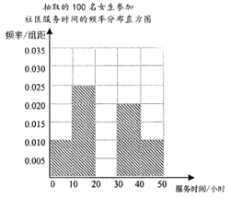
(1)完善男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.
抽取的100名男生参加社区服务时间的频率分布表
社区服务时间 | 人数 | 频率 |
| 0.05 | |
| 20 | |
| 0.35 | |
| 30 | |
| ||
合计 | 100 | 1 |
学生社区服务时间合格与性别的列联表
不合格的人数 | 合格的人数 | |
男 | ||
女 |
(2)按高中综合素质评价的要求,高中学生每年参加社区服务的时间不少于20个小时才为合格,根据上面的统计图表,完成抽取的这200名学生参加社区服务时间合格与性别的列联表,并判断是否有![]() 以上的把握认为参加社区服务时间达到合格程度与性别有关,并说明理由.
以上的把握认为参加社区服务时间达到合格程度与性别有关,并说明理由.
(3)用以上这200名学生参加社区服务的时间估计全市9万名高中学生参加社区服务时间的情况,并以频率作为概率.
(i)求全市高中学生参加社区服务时间不少于30个小时的人数.
(ⅱ)对我市高中生参加社区服务的情况进行评价.
参考公式
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.002 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(![]() ,其
,其![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com