
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:

(1)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程;
(2)据(1)的结果估计当销售额为1亿元时的利润额.
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() ,曲线
,曲线![]() :
:![]() (
(![]() 为参数), 以坐标原点
为参数), 以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() :
:![]() (
(![]() )分别交
)分别交![]() ,
,![]() 于
于![]() 两点, 求
两点, 求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为![]() ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
(1)求甲同学至少有4次投中的概率;
(2)求乙同学投篮次数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,用茎叶图表示如下图:
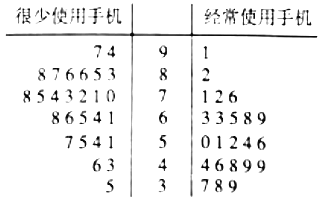
(1)根据茎叶图中的数据完成下面的![]() 列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
及格( | 不及格 | 合计 | |
很少使用手机 | |||
经常使用手机 | |||
合计 |
(2)从50人中,选取一名很少使用手机的同学记为甲和一名经常使用手机的同学记为乙,解一道数列题,甲、乙独立解决此题的概率分别为![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,则此二人适合结为学习上互帮互助的“师徒”,记
,则此二人适合结为学习上互帮互助的“师徒”,记![]() 为两人中解决此题的人数,若
为两人中解决此题的人数,若![]() ,问两人是否适合结为“师徒”?
,问两人是否适合结为“师徒”?
参考公式及数据: 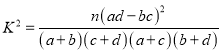 ,其中
,其中![]() .
.
| <>0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系![]() 中曲线
中曲线![]() 经伸缩变换
经伸缩变换![]() 后得到曲线
后得到曲线![]() ,在以
,在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的参数方程和
的参数方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的一点,又
上的一点,又![]() 向曲线
向曲线![]() 引切线,切点为
引切线,切点为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),其中0<α<β<π.
=(cosβ,sinβ),其中0<α<β<π.
(1)求证: ![]() 与
与 ![]() 互相垂直;
互相垂直;
(2)若k ![]() 与
与 ![]() ﹣k
﹣k ![]() 的长度相等,求β﹣α的值(k为非零的常数).
的长度相等,求β﹣α的值(k为非零的常数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点坐标分别是
的两个焦点坐标分别是![]() ,并且经过
,并且经过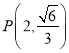 .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的右焦点
的右焦点![]() 作直线
作直线![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,当
两点,当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个动圆与已知圆Q1:(x+2)2+y2=![]() 外切,与圆Q2:(x-2)2+y2=
外切,与圆Q2:(x-2)2+y2=![]() 内切,(1) 试求这个动圆圆心的轨迹方程;(2)设直线
内切,(1) 试求这个动圆圆心的轨迹方程;(2)设直线![]() 与(1)中动圆圆心轨迹交于A、B两点,坐标原点O到直线
与(1)中动圆圆心轨迹交于A、B两点,坐标原点O到直线![]() 的距离为
的距离为![]() ,求△AOB面积的最大值。
,求△AOB面积的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com