
【题目】已知函数f(x)=ln(![]() ﹣3x)+1,则f(lg2)+f(lg
﹣3x)+1,则f(lg2)+f(lg![]() )=( )
)=( )
A.-1
B.0
C.1
D.2
【答案】D
【解析】解:因为函数g(x)=ln(![]() ﹣3x)满足g(﹣x)=ln(
﹣3x)满足g(﹣x)=ln(![]() +3x)=﹣ln(
+3x)=﹣ln(![]() ﹣3x)=﹣g(x),函数是奇函数,g(lg2)+g(﹣lg2)=0,
﹣3x)=﹣g(x),函数是奇函数,g(lg2)+g(﹣lg2)=0,
所以f(lg2)+f(lg![]() )=f(lg2)+f(﹣lg2)=0+1+1=2.
)=f(lg2)+f(﹣lg2)=0+1+1=2.
故选:D.
【考点精析】认真审题,首先需要了解函数奇偶性的性质(在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇),还要掌握函数的值(函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法)的相关知识才是答题的关键.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
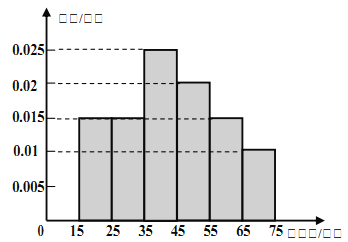
【题目】2016年5月20日,针对部分“二线城市”房价上涨过快,媒体认为国务院常务会议可能再次确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了![]() 人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如下表):
人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如下表):
月收入(百元) | 赞成人数 |
|
|
|
|
|
|
|
|
|
|
|
|
(1)试根据频率分布直方图估计这![]() 人的中位数和平均月收入;
人的中位数和平均月收入;
(2)若从月收入(单位:百元)在![]() 的被调查者中随机选取
的被调查者中随机选取![]() 人进行追踪调查,求被选取的
人进行追踪调查,求被选取的![]() 人都不赞成的概率.
人都不赞成的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点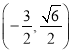 ,顺次连接椭圆的四个顶点得到的四边形的面积为
,顺次连接椭圆的四个顶点得到的四边形的面积为![]() ,点
,点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)已知点![]() ,是椭圆
,是椭圆![]() 上的两点.
上的两点.
(ⅰ)若![]() ,且
,且![]() 为等边三角形,求
为等边三角形,求![]() 的面积;
的面积;
(ⅱ)若![]() ,证明:
,证明: ![]() 不可能为等边三角形.
不可能为等边三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方体ABCD﹣A1B1C1D1中,AB=2,AA1=AD=4,点E为AB中点.
(1)求证:BD1∥平面A1DE;
(2)求证:A1D⊥平面ABD1 . 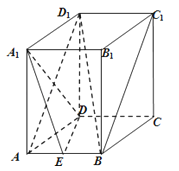
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015 年 12 月,华中地区数城市空气污染指数“爆表”,此轮污染为 2015 年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)利用(1)所求的回归方程,预测该市车流量为 12 万辆时![]() 的浓度.
的浓度.
参考公式:回归直线的方程是![]() ,
,
其中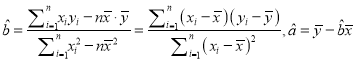 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点C(t,![]() ) (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
) (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y﹣4=0与圆C交于点M、N,若OM=ON,求圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中正确的个数是( ) (1.)若x∈R,则x2+ ![]() ≥x;
≥x;
(2.)若x≠kπ,k∈Z,则sinx+ ![]() ≥2;
≥2;
(3.)设x,y>0,则 ![]() 的最小值为8;
的最小值为8;
(4.)设x>1,则x+ ![]() 的最小值为3.
的最小值为3.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四边形ABCD,AB=BD=DA=2.BC=CD= ![]() ,现将△ABD沿BD折起,使二面角A﹣BD﹣C的大小在[
,现将△ABD沿BD折起,使二面角A﹣BD﹣C的大小在[ ![]() ,
, ![]() ],则直线AB与CD所成角的余弦值取值范围是( )
],则直线AB与CD所成角的余弦值取值范围是( ) 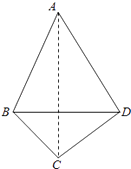
A.[0, ![]() ]∪(
]∪( ![]() ,1)
,1)
B.[ ![]() ,
, ![]() ]
]
C.[0, ![]() ]
]
D.[0, ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com