
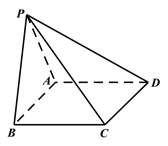
【题目】如图,四棱锥![]() 的底面
的底面![]() 为平行四边形,平面
为平行四边形,平面![]() 平面
平面![]() ,
, ![]() ,
,![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)若三角形![]() 是边长为
是边长为![]() 的等边三角形,求三棱锥
的等边三角形,求三棱锥![]() 外接球的表面积.
外接球的表面积.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)本问证明线线垂直,可以先证线面垂直,再证线线垂直,即证明AB垂直于PC所在平面,过P作![]() 于
于![]() ,根据面面垂直性质定理可知,PO
,根据面面垂直性质定理可知,PO![]() 面
面![]() ,易知PO
,易知PO![]() AB,再证明OC
AB,再证明OC![]() AB即可;(Ⅱ)求三棱锥
AB即可;(Ⅱ)求三棱锥![]() 的外接球,关键是找到外接球的球心,因为三角形
的外接球,关键是找到外接球的球心,因为三角形![]() 是边长为
是边长为![]() 的等边三角形,设E为三角形
的等边三角形,设E为三角形![]() 的重心,显然EP=EA=EB,再通过证明EC=EB,于是可以得出EA=EB=EC=EP,则可以说明E为外接球的球心,于是可以求外接球半径,再求三棱锥
的重心,显然EP=EA=EB,再通过证明EC=EB,于是可以得出EA=EB=EC=EP,则可以说明E为外接球的球心,于是可以求外接球半径,再求三棱锥![]() 外接球的表面积.
外接球的表面积.
试题解析: (Ⅰ)作![]() 于
于![]() ……①,连接
……①,连接![]() ,
,
∵平面![]() 平面
平面![]() ,且
,且![]() ,
,
∴![]() 面
面![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ……②
……②
又![]() ,由①②,得
,由①②,得![]() 面
面![]() ,
,
又![]() 面
面![]() ,∴
,∴![]() .
.
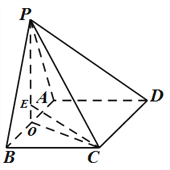
(Ⅱ)∵三角形![]() 是边长为
是边长为![]() 的等边三角形,∴
的等边三角形,∴![]() .
.
∵![]() 面
面![]() ,
, ![]() ,线段
,线段![]() 上取点
上取点![]() ,∴
,∴![]() ,
,
![]() 是外接球的球心,设三棱锥
是外接球的球心,设三棱锥![]() 外接球的半径为
外接球的半径为![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】已知动点![]() 到直线
到直线![]() 的距离是它到点
的距离是它到点![]() 的距离的
的距离的![]() 倍.
倍.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设轨迹![]() 上一动点
上一动点![]() 满足:
满足: ![]() ,其中
,其中![]() 是轨迹
是轨迹![]() 上的点,且直线
上的点,且直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,若
,若![]() 为一动点,
为一动点, 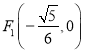 ,
, 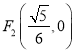 为两定点,求
为两定点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2![]() , AD=2,求四边形绕AD旋转一周所围成几何体的表面积及体积.
, AD=2,求四边形绕AD旋转一周所围成几何体的表面积及体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数y=g(x)满足:g(2)=4,定义域为R的函数f(x)=![]() 是奇函数.
是奇函数.
(1)确定y=g(x)的解析式;
(2)求m,n的值;
(3)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面为平行四边形的四棱锥P﹣ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
(Ⅰ)求证:AC⊥PB;
(Ⅱ)求证:PB∥平面AEC.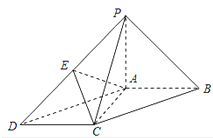
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A={x|2x2+ax+2=0},B={x|x2+3x﹣b=0},且A∩B={2}.
(1)求a,b的值;
(2)设全集U=AUB,求(UA)U(UB).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com