
已知函数f(x)=(x-1)2,g(x)=4(x-1),数列{an}是各项均不为0的等差数列,其前n项和为Sn,点(an+1,S2n-1)在函数f(x)的图象上;数列{bn}满足b1=2,bn≠1,且(bn-bn+1)·g(bn)=f(bn)(n∈N+).
(1)求an并证明数列{bn-1}是等比数列;
(2)若数列{cn}满足cn=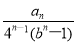 ,证明:c1+c2+c3+…+cn<3.
,证明:c1+c2+c3+…+cn<3.
见解析
【解析】(1)因为点(an+1,S2n-1)在函数f(x)的图象上,所以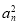 =S2n-1.
=S2n-1.
令n=1,n=2,得 即
即 解得a1=1,d=2(d=-1舍去),则an=2n-1.
解得a1=1,d=2(d=-1舍去),则an=2n-1.
由(bn-bn+1)·g(bn)=f(bn),
得4(bn-bn+1)(bn-1)=(bn-1)2.
由题意bn≠1,所以4(bn-bn+1)=bn-1,
即3(bn-1)=4(bn+1-1),所以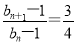
所以数列{bn-1}是以1为首项,公比为 的等比数列.
的等比数列.
(2)由(1),得bn-1=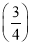 n-1.cn=
n-1.cn=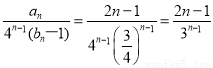 .
.
令Tn=c1+c2+c3+…+cn,
则Tn=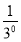 +
+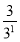 +
+ +…+
+…+ +
+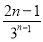 ,①
,①
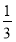 Tn=
Tn= +
+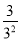 +
+ +…+
+…+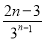 +
+ ,②
,②
①-②得,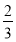 Tn=
Tn=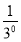 +
+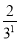 +
+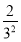 +
+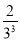 +…+
+…+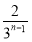 -
- =1+
=1+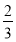 ·
·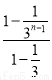 -
-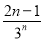 =2-
=2-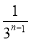 -
-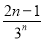 =2-
=2-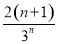 .所以Tn=3-.
.所以Tn=3-.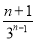
所以c1+c2+c3+…+cn=3-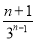 <3.
<3.


科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:选择题
某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是( ).
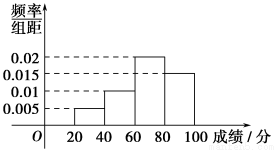
A.45 B.50 C.55 D.60
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:填空题
已知ABCD-A1B1C1D1为正方体,①( +
+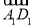 +
+ )2=3
)2=3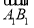 2;②
2;② ·(
·(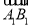 -
-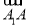 )=0;③向量
)=0;③向量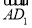 与向量
与向量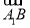 的夹角是60°;④正方体ABCD-A1B1C1D1的体积为|
的夹角是60°;④正方体ABCD-A1B1C1D1的体积为|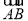 ·
·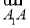 ·
·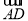 |.其中正确命题的序号是________.
|.其中正确命题的序号是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(解析版) 题型:解答题
已知四棱锥P?ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC,AD的中点.
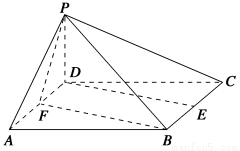
(1)求证:DE∥平面PFB;
(2)已知二面角P?BF?C的余弦值为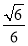 ,求四棱锥P?ABCD的体积.
,求四棱锥P?ABCD的体积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(解析版) 题型:选择题
某四棱台的三视图如图所示,则该四棱台的体积是( ).
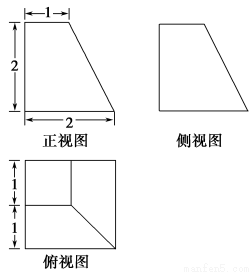
A.4 B. 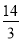 C.
C.  D.6
D.6
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:选择题
已知函数f(x)=cos x(x∈(0,2π))有两个不同的零点x1,x2,方程f(x)=m有两个不同的实根x3,x4.若把这四个数按从小到大排列构成等差数列,则实数m的值为( ).
A.-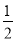 B.
B.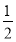 C.
C.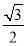 D.-
D.-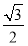
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,椭圆C: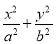 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为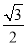 ,以坐标原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
,以坐标原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
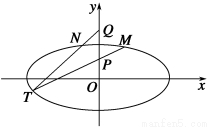
(1)求椭圆C的方程;
(2)已知点P(0,1),Q(0,2),设M,N是椭圆C上关于y轴对称的不同两点,直线PM与QN相交于点T.求证:点T在椭圆C上.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(解析版) 题型:解答题
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=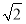 .
.
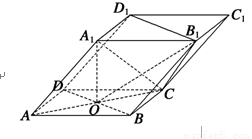
(1)证明:A1C⊥平面BB1D1D;
(2)求平面OCB1与平面BB1D1D的夹角θ的大小.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷2练习卷(解析版) 题型:选择题
已知向量a,b满足|a|=2,|b|=1,且(a+b)⊥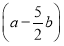 ,则a与b的夹角为( ).
,则a与b的夹角为( ).
A.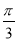 B.
B.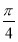 C.
C.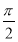 D.
D.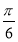
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com