
【题目】某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的比例 |
第1组 | [18,28) | 5 | 0.5 |
第2组 | [28,38) | 18 | a |
第3组 | [38,48) | 27 | 0.9 |
第4组 | [48,58) | x | 0.36 |
第5组 | [58,68) | 3 | 0.2 |
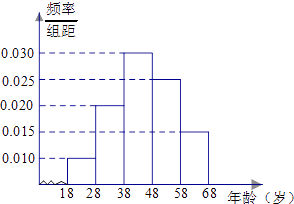
(1)分别求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
【答案】
(1)解:第1组人数5÷0.5=10,所以n=10÷0.1=100,
第2组频率为:0.2,人数为:100×0.2=20,所以a=18÷20=0.9,
第4组人数100×0.25=25,所以x=25×0.36=9
(2)解:第2,3,4组回答正确的人的比为18:27:9=2:3:1,所以第2,3,4组每组应各依次抽取2人,3人,1人.
(3)解:记“所抽取的人中第2组至少有1人获得幸运奖”为事件A,抽取的6人中,第2组的设为a1,a2,第3组的设为b1,b2,b3,第4组的设为c,则从6名幸运者中任取2名的所有可能的情况有15种,它们是:(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,c),(a2,b1),(a2,b2),(a2,b3),(a2,c),(b1,b2),(b1,b3),(b1,c),(b2,b3),(b2,c),(b3,c).…(11分)
其中第2组至少有1人的情况有9种,他们是:(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,c),(a2,b1),
(a2,b2),(a2,b3),(a2,c).
∴P(A)= ![]() .
.
答:所抽取的人中第2组至少有1人获得幸运奖的概率为 ![]()
【解析】(1)由回答对的人数:每组的人数=回答正确的概率,分别可求得要求的值;(2)由分层抽样按比例抽取的特点可得各组的人数;(3)记抽取的6人中,第2组的记为a1 , a2 , 第3组的记为b1 , b2 , b3 , 第4组的记为c,列举可得从6名学生中任取2名的所有可能的情况,以及其中第2组至少有1人的情况种数,由古典概型可得概率.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.
(Ⅰ) 证明:BM⊥平面AEC;
(Ⅱ) 求MC与平面DEC所成的角的余弦值.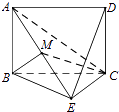
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,若函数
时,若函数![]() 的导函数
的导函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,其横坐标分别为
两点,其横坐标分别为![]() ,
, ![]() ,线段
,线段![]() 的中点的横坐标为
的中点的横坐标为![]() ,且
,且![]() ,
, ![]() 恰为函数
恰为函数![]() 的零点,求证:
的零点,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中, ![]() 与
与![]() 相交于点
相交于点![]() ,
, ![]() 平面
平面![]() ,
, ![]() .
.

(I)求证: ![]() 平面
平面![]() ;
;
(II)当直线![]() 与平面
与平面![]() 所成的角的余弦值为
所成的角的余弦值为![]() 时,求证:
时,求证: ![]() ;
;
(III)在(II)的条件下,求异面直线![]() 与
与![]() 所成的余弦值.
所成的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】福利彩票“双色球”中红球的号码可以从01,02,03,…,32,33这33个二位号码中选取,小明利用如图所示的随机数表选取红色球的6个号码,选取方法是从第1行第9列和第10列的数字开始从左到右依次选取两个数字,则第四个被选中的红色球号码为( )
81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 85 |
06 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49 |
A. 12 B. 33 C. 06 D. 16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体ABCD﹣A1B1C1D1中,M,N分别为棱AB,DD1的中点,异面直线A1M和C1N所成的角为( ) 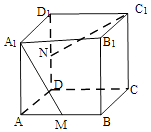
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求满足下列条件的椭圆方程:
(1)长轴在x轴上,长轴长等于12,离心率等于 ![]() ;
;
(2)椭圆经过点(﹣6,0)和(0,8);
(3)椭圆的一个焦点到长轴两端点的距离分别为10和4.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com