
某市环保局为增加城市的綠地面积,提出两个投资方案:方案A为一次性投资100万元;方案B为第一年投资10 万元,以后每年都比前一年增加10万元。则按照方案B经过多少年后,总投入不少于方案A的投入。答曰:( )
| A.4 | B.5 | C.9 | D.10 |
科目:高中数学 来源: 题型:单选题
若数列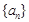 满足:存在正整数
满足:存在正整数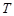 ,对于任意正整数
,对于任意正整数 都有
都有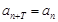 成立,则称数列
成立,则称数列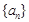 为周期数列,周期为
为周期数列,周期为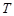 . 已知数列
. 已知数列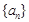 满足
满足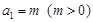 ,
,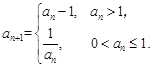
则下列结论中错误的是( )
A.若m=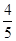 ,则a5=3 ,则a5=3 |
| B.若a3=2,则m可以取3个不同的值 |
C.若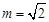 ,则数列 ,则数列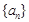 是周期为 是周期为 的数列 的数列 |
D.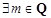 且 且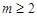 ,数列 ,数列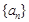 是周期数列 是周期数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
一个赛跑机器人有如下特性:
(1)步长可以人为地设置成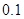 米,
米,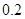 米,
米,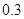 米,…,
米,…,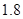 米或
米或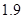 米;
米;
(2)发令后,机器人第一步立刻迈出设置的步长,且每一步的行走过程都在瞬时完成;
(3)当设置的步长为 米时,机器人每相邻两个迈步动作恰需间隔
米时,机器人每相邻两个迈步动作恰需间隔 秒.
秒.
则这个机器人跑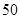 米(允许超出
米(允许超出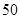 米)所需的最少时间是【 】.
米)所需的最少时间是【 】.
A.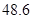 秒 秒 | B.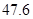 秒 秒 | C.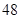 秒 秒 | D.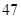 秒 秒 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知数列{an}的通项公式为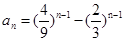 ,则数列{an}
,则数列{an}
| A.有最大项,没有最小项 | B.有最小项,没有最大项 |
| C.既有最大项又有最小项 | D.既没有最大项也没有最小项 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com