练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

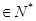    数列满足，且对任意的都有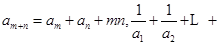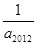：等于   (     )

    A．B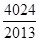．C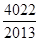．D．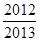

    B

    解析试题分析：令，则，所以，所以
    …，，以上个式子相加，得整理得，所以，
    所以
    考点：本小题主要考查累加法求数列的通项公式、裂项相消法求数列的前n项和，考查学生的转化能力和运算求解能力.
    点评：由数列的递推公式求通项公式需要掌握累加、累乘和构造新数列三种方法，而求数列的前n项和主要有公式法、分组法、裂项相消法和错位相减法等，其中裂项相消法和错位相减法是考查的重点.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：单选题

    已知数列的通项公式，则数列的前项和的最小值是（  ）

    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知数列的，且，则此数列的通项公式为（    ）

    A．B．
    C．D．或

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如图所示的三角形数阵叫“莱布尼兹调和三角形”，它们是由整数的倒数组成的，第行有个数且两端的数均为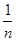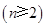，每个数是它下一行左右相邻两数的和，如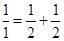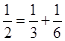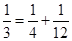，，，…，则第7行第4个数（从左往右数）为(   )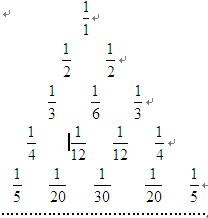

    A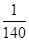． B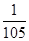． C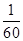． D．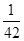

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知数列，，，且，则数列的第五项为（   ）

    A． B． C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    实数成等差数列，成等比数列，则的大小关系是（   ）

    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    某市环保局为增加城市的綠地面积，提出两个投资方案：方案A为一次性投资100万元；方案B为第一年投资10 万元，以后每年都比前一年增加10万元。则按照方案B经过多少年后，总投入不少于方案A的投入。答曰：(     )

    A．4B．5 C．9D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知数列满足：（m为正整数），若，则m所有可能的取值为________。

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    若数列满足：，则该数列的通项公式＝__________。

    查看答案和解析>>

    同步练习册答案