
(1)已知 ,求证:
,求证: ;
;
(2)已知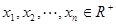 ,且
,且 ,
,
求证: .
.
证明见解析.
解析试题分析:(1)本题证明只要利用作差法即可证得;(2)这个不等式比较复杂,考虑到不等式的形式,我们可用数学归纳法证明,关键在 时的命题如何应用
时的命题如何应用 时的结论,
时的结论, 中要把两个括号合并成一个,又能应用
中要把两个括号合并成一个,又能应用 时的结论证明
时的结论证明 时的结论,当
时的结论,当 时,结论已经成立,当
时,结论已经成立,当 时,在
时,在 中可找到一个,不妨设为
中可找到一个,不妨设为 ,使
,使 ,即
,即 ,从而有
,从而有


 ,这样代入进去可证得
,这样代入进去可证得 时结论成立.
时结论成立.
(1)因为 ,所以
,所以 ,即
,即 ; 2分
; 2分
(2)证法一(数学归纳法):(ⅰ)当 时,
时, ,不等式成立. 4分
,不等式成立. 4分
(ⅱ)假设 时不等式成立,即
时不等式成立,即 成立. 5分
成立. 5分
则 时,若
时,若 ,则命题成立;若
,则命题成立;若 ,则
,则 中必存在一个数小于1,不妨设这个数为
中必存在一个数小于1,不妨设这个数为 ,从而
,从而 ,即
,即 .
. 同理可得,
同理可得,
所以





故 时,不等式也成立. 9分
时,不等式也成立. 9分
由(ⅰ)(ⅱ)及数学归纳法原理知原不等式成立. 10分
证法二:(恒等展开)左右展开,得
 由平均值不等式,得
由平均值不等式,得
 8分
8分
故

 . 10分
. 10分
考点:(1)比较法证不等式;(2)数学归纳法证不等式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
给出四个等式:
1=1
1-4=-(1+2)
1-4+9=1+2+3
1-4+9-16=-(1+2+3+4)
……
(1)写出第5,6个等式,并猜测第n(n∈N*)个等式
(2)用数学归纳法证明你猜测的等式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga (其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与
(其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
在解决问题:“证明数集 没有最小数”时,可用反证法证明.
没有最小数”时,可用反证法证明.
假设 是
是 中的最小数,则取
中的最小数,则取 ,可得:
,可得: ,与假设中“
,与假设中“ 是
是 中的最小数”矛盾!那么对于问题:“证明数集
中的最小数”矛盾!那么对于问题:“证明数集 没有最大数”,也可以用反证法证明.我们可以假设
没有最大数”,也可以用反证法证明.我们可以假设 是
是 中的最大数,则可以找到
中的最大数,则可以找到 ▲ (用
▲ (用 ,
, 表示),由此可知
表示),由此可知 ,
, ,这与假设矛盾!所以数集
,这与假设矛盾!所以数集 没有最大数.
没有最大数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com