
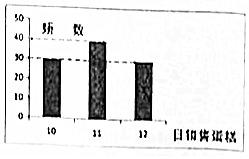
 某超市每两天购入一批某型号的生日蛋糕进行销售,进价50元/个,售价60元/个,若每次购入的生日蛋糕两天内没有售完,则以40元/个的价格可以全部处理掉,根据此超市以往随机抽取的100天此类蛋糕的销售情况,如柱形图所示.设n为每次购入的蛋糕数,ξ为两天内的蛋糕销售数量,W为此批购入的蛋糕销售的利润(视频率为概率,且每天销售情况是独立的)
某超市每两天购入一批某型号的生日蛋糕进行销售,进价50元/个,售价60元/个,若每次购入的生日蛋糕两天内没有售完,则以40元/个的价格可以全部处理掉,根据此超市以往随机抽取的100天此类蛋糕的销售情况,如柱形图所示.设n为每次购入的蛋糕数,ξ为两天内的蛋糕销售数量,W为此批购入的蛋糕销售的利润(视频率为概率,且每天销售情况是独立的)分析 (1)由题意,ξ为两天内的蛋糕销售数量,从柱形图的日销售量可得ξ的可能取值.
(2)视频率为概率,由柱形图的日销售量可知:日销售量为12个的有30天,其概率=$\frac{30}{100}=\frac{3}{10}$,
可得ξ≤22的概率P=1-$\frac{3}{10}$=$\frac{7}{10}$.
(3)当n=22时,即两天内的蛋糕销售数量为:10个和12个进行讨论,可得利润W.
解答 解:(1)由题意,ξ为两天内的蛋糕销售数量,
从柱形图的日销售量可得:ξ可取:ξ=10+11=21,ξ=10+12=22,ξ=11+12=23,
∴ξ的可能取值的集合为{21,22,23}.
(2)由柱形图的日销售量可知:日销售量为12个的有30天,其概率=$\frac{30}{100}=\frac{3}{10}$,
∴ξ≤22的概率P=1-$\frac{3}{10}$=$\frac{7}{10}$.
(3)当n=22时,即两天内的蛋糕销售数量为:10个和12个,
当第一天销售数量为10个时,第二天销售数量为10个时,其利润W=20(60-50)+2(40-50)=180.
当第一天销售数量为12个时,第二天销售数量为10个时,其利润W=22(60-50=220.
点评 本题考了对题意的理解和运用,情况的讨论.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com