
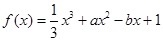 (
(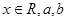 为实数)有极值,且在
为实数)有极值,且在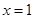 处的切线与直线
处的切线与直线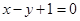 平行.
平行.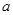 的取值范围;
的取值范围;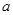 ,使得函数
,使得函数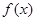 的极小值为1,若存在,求出实数
的极小值为1,若存在,求出实数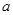 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;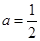 ,
,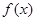 的导数为
的导数为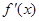 ,令
,令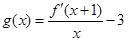
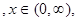
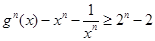
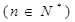
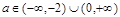 ;
;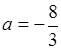 ,使得函数f(x)的极小值为1 ;
,使得函数f(x)的极小值为1 ;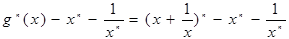
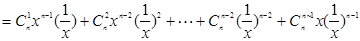
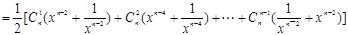
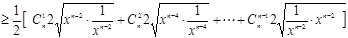
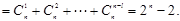
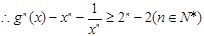
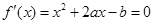 有两个不同的实数根,从而得到b,a的一个不等式,再根据
有两个不同的实数根,从而得到b,a的一个不等式,再根据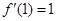 得到a,b的等式,消去b,可以解出a的取值范围.
得到a,b的等式,消去b,可以解出a的取值范围.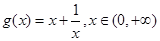 ,然后问题的关键是
,然后问题的关键是 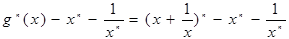
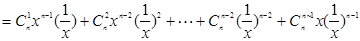
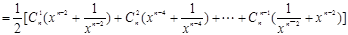
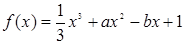 ,∴
,∴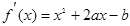 ,由题意∴f/(1)=1+2a-b=1,
,由题意∴f/(1)=1+2a-b=1,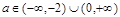 4分
4分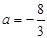 .……………5分
.……………5分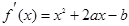 ,令f/(x)=0
,令f/(x)=0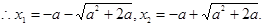

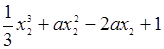 =1,
=1,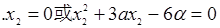 ……………………………………………………7分
……………………………………………………7分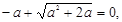 则a=0(舍).……………………8分
则a=0(舍).……………………8分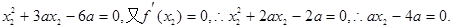
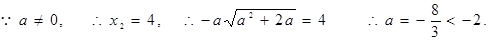
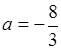 ,使得函数f(x)的极小值为1 ………9分
,使得函数f(x)的极小值为1 ………9分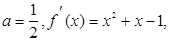
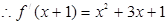 ,
, 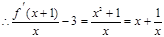
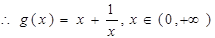 …….l0分
…….l0分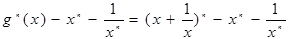
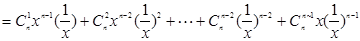
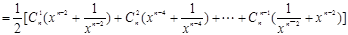
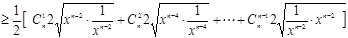
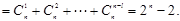
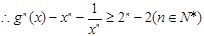 …………………………………………14分
…………………………………………14分

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com