练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

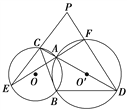
    【题目】如图所示，⊙O与⊙O′相交于A、B两点，过A引直线CD，EF分别交两圆于点C、D、E、F，EC与DF的延长线相交于点P，求证：∠P＋∠CBD＝180°.

    【答案】见解析

    【解析】试题分析：所对的圆周角相等，得到∠E＝∠CBA. 又四边形ABDF内接于⊙O′，所以∠PFA＝∠ABD，所以∠E＋∠PFE＝∠CBA＋∠ABD＝∠CBD.又因为∠E＋∠P＋∠PFE＝180°，所以∠P＋∠CBD＝180°.

    试题解析：

    证明：如图所示，连接AB，因为∠E与∠CBA是圆O中所对的圆周角，

    所以∠E＝∠CBA.

    又四边形ABDF内接于⊙O′，

    所以∠PFA＝∠ABD，

    所以∠E＋∠PFE＝∠CBA＋∠ABD＝∠CBD.

    又因为∠E＋∠P＋∠PFE＝180°，

    所以∠P＋∠CBD＝180°.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】近年来随着我国在教育科研上的投入不断加大，科学技术得到迅猛发展,国内企业的国际竞争力得到大幅提升.伴随着国内市场增速放缓，国内有实力企业纷纷进行海外布局，第二轮企业出海潮到来.如在智能手机行业,国产品牌已在赶超国外巨头，某品牌手机公司一直默默拓展海外市场，在海外共设多个分支机构，需要国内公司外派大量后、后中青年员工.该企业为了解这两个年龄层员工是否愿意被外派工作的态度，按分层抽样的方式从后和后的员工中随机调查了位，得到数据如下表：

    愿意被外派

    不愿意被外派

    合计

    后

    后

    合计

    /p>

    （Ⅰ）根据调查的数据，是否有以上的把握认为“是否愿意被外派与年龄有关”，并说明理由；

    （Ⅱ）该公司举行参观驻海外分支机构的交流体验活动，拟安排名参与调查的后、后员工参加.后员工中有愿意被外派的人和不愿意被外派的人报名参加，从中随机选出人，记选到愿意被外派的人数为；后员工中有愿意被外派的人和不愿意被外派的人报名参加，从中随机选出人，记选到愿意被外派的人数为，求的概率．

    参考数据：

    （参考公式：，其中）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面为直角梯形， ， ， 垂直于底面， ， ， 分别为， 的中点．

    （Ⅰ）求证： ；

    （Ⅱ）求四棱锥的体积和截面的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆的圆心坐标，直线：被圆截得弦长为。

    （Ⅰ）求圆的方程；

    （Ⅱ）从圆外一点向圆引切线，求切线方程。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着手机的发展，“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查，随机抽取了50人，他们年龄的频数分布及对“使用微信交流”赞成人数如下表.

    年龄（单位：岁）

    [15,25）

    [25,35）

    [35,45）

    [45,55）

    [55,65）

    [65,75）

    频数

    5

    10

    15

    10

    5

    5

    赞成人数

    5

    10

    12

    7

    2

    1

    （Ⅰ）若以“年龄45岁为分界点”，由以上统计数据完成下面列联表，并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关；

    年龄不低于45岁的人数

    年龄低于45岁的人数

    合计

    赞成

    不赞成

    合计

    （Ⅱ）若从年龄在[25,35）和[55,65）的被调查人中按照分层抽样的方法选取6人进行追踪调查，并给予其中3人“红包”奖励，求3人中至少有1人年龄在[55,65）的概率.

    参考数据如下：

    附临界值表：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    的观测值： （其中）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数y=f（x）同时满足：（ⅰ）对于定义域内的任意x，恒有f（x）+f（﹣x）=0；（ⅱ）对于定义域内的任意x1 ， x2 ， 当x1≠x2时，恒有 ， 则称函数f（x）为“二维函数”．现给出下列四个函数：
    ①f（x）=
    ②f（x）=﹣x3+x
    ③
    ④
    其中能被称为“二维函数”的有 （写出所有满足条件的函数的序号）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校从高一年级学生中随机抽取40名中学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成六段： ， ，…， ，得到如图所示的频率分布直方图.

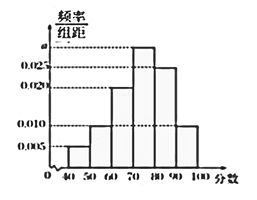
    （1）求图中实数的值；

    （2）若该校高一年级共有640人，试估计该校高一年级期中考试数学成绩不低于60分的人数；

    （3）若从数学成绩在与两个分数段内的学生中随机选取2名学生，求这2名学生的数学成绩之差的绝对值不大于10的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： 的左焦点，若椭圆上存在一点，满足以椭圆短轴为直径的圆与线段相切于线段的中点.

    （1）求椭圆的方程；

    （2）过坐标原点的直线交椭圆： 于、两点，其中点在第一象限，过作轴的垂线，垂足为，连结并延长交椭圆于，求证： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆： 和点，动圆经过点且与圆相切，圆心的轨迹为曲线．

    （1）求曲线的方程；

    （2）点是曲线与轴正半轴的交点，点， 在曲线上，若直线， 的斜率分别是， ，满足，求面积的最大值．

    查看答案和解析>>

    同步练习册答案