
【题目】某校从高一年级学生中随机抽取40名中学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段: ![]() ,
, ![]() ,…,
,…, ![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
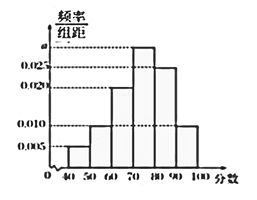
(1)求图中实数![]() 的值;
的值;
(2)若该校高一年级共有640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在![]() 与
与![]() 两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
【答案】(1) ![]() ;(2) 高一年级数学成绩不低于60分的人数约为
;(2) 高一年级数学成绩不低于60分的人数约为![]() 人;(3) 这两名学生的数学成绩之差的绝对值不大于10的概率为
人;(3) 这两名学生的数学成绩之差的绝对值不大于10的概率为![]() .
.
【解析】试题分析:(1)根据图中所有小矩形的面积之和等于1建立关于a的等式,解之即可求出所求;
(2)根据频率分布直方图,成绩不低于60分的频率,然后根据频数=频率×总数可求出所求;
(3)成绩在[40,50)分数段内的人数,以及成绩在[90,100]分数段内的人数,列出所有的基本事件,以及两名学生的数学成绩之差的绝对值不大于10的基本事件,最后利用古典概型的概率公式解之即可.
试题解析:
(1)由于图中所有小矩形的面积之和等于1,所以10×(0.005+0.01+0.02+a+0.025+0.01)=1.
解得a=0.03
(2)根据频率分布直方图,成绩不低于60分的频率为110×(0.005+0.01)=0.85由于该校高一年级共有学生640人,利用样本估计总体的思想,可估计该校高一年级数学成绩不低于60分的人数约为640×0.85=544人
(3)成绩在[40,50)分数段内的人数为40×0.05=2人,分别记为A,B,成绩在[90,100]分数段内的人数为40×0.1=4人,分别记为C,D,E,F.
若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,则所有的基本事件有:(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共15种.…(9分)
如果两名学生的数学成绩都在[40,50)分数段内或都在[90,100]分数段内,那么这两名学生的数学成绩之差的绝对值一定不大于10.如果一个成绩在[40,50)分数段内,另一个成绩在[90,100]分数段内,那么这两名学生的数学成绩之差的绝对值一定大于10.
记“这两名学生的数学成绩之差的绝对值不大于10”为事件M,则事件M包含的基本事件有:(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共7种.所以所求概率为P(M)= ![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知a,b,c为△ABC的三个内角A,B,C的对边,向量![]() =(
=(![]() , ﹣1),
, ﹣1),![]() =(cosA,sinA).若
=(cosA,sinA).若![]() ⊥
⊥![]() , 且αcosB+bcosA=csinC,则角A,B的大小分别为( )
, 且αcosB+bcosA=csinC,则角A,B的大小分别为( )
A.![]() ,
,![]()
B.![]() ,
,![]()
C.![]() ,
,![]()
D.![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO与直线CD相交于点F.
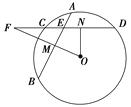
证明:(1)∠MEN+∠NOM=180°;
(2)FE·FN=FM·FO.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为
的定义域为![]() ,对给定的正数
,对给定的正数![]() ,若存在闭区间
,若存在闭区间![]() ,使得函数
,使得函数![]() 满足:①
满足:①![]() 在
在![]() 内是单调函数;②
内是单调函数;②![]() 在
在![]() 上的值域为
上的值域为![]() ,则称区间
,则称区间![]() 为
为![]() 的
的![]() 级“理想区间”.下列结论错误的是( )
级“理想区间”.下列结论错误的是( )
A. 函数![]() (
(![]() )存在1级“理想区间”
)存在1级“理想区间”
B. 函数![]() (
(![]() )不存在2级“理想区间”
)不存在2级“理想区间”
C. 函数![]() (
(![]() )存在3级“理想区间”
)存在3级“理想区间”
D. 函数![]() ,
, ![]() 不存在4级“理想区间”
不存在4级“理想区间”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数![]()
(1)若![]() 在
在![]() 处取得极值,确定
处取得极值,确定![]() 的值,并求此时曲线
的值,并求此时曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上为减函数,求
上为减函数,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 是正方形,
是正方形, ![]() .
.
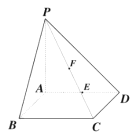
(1)求异面直线![]() 与
与![]() 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)求点![]() 、
、![]() 分别是棱
分别是棱![]() 和
和![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,二次函数
中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() .当
.当![]() 变化时,解答下列问题:
变化时,解答下列问题:
(1)以![]() 为直径的圆能否经过点
为直径的圆能否经过点![]() ?说明理由;
?说明理由;
(2)过![]() ,
, ![]() ,
, ![]() 三点的圆在
三点的圆在![]() 轴上截得的弦长是否为定值?若是,则求出该定值;若不是,请说明理由.
轴上截得的弦长是否为定值?若是,则求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com