【题目】已知数列
为等比数列， 
，公比
，且
成等差数列.
（1）求数列
的通项公式；
（2）设
， 
，求使
的
的值.
【答案】（1）
；（2）
.
【解析】试题分析：（1）由
成等差数列，知
，由
为等比数列，且
，故
，由此能求出数列
的通项公式；（2）由
，知
，由此利用裂项求和法能够求出由
的
的取值.
试题解析：（1）由
成等差数列，得
，
又为等比数列，且
，
故
，解得
，
又
， 
，
（2）
，
，
，
故由
，可得
.
【方法点晴】本题主要考查等比数列的通项公式基本量运算，以及裂项相消法求数列的和，属于中档题. 裂项相消法是最难把握的求和方法之一，其原因是有时很难找到裂项的方向，突破这一难点的方法是根据式子的结构特点，常见的项技巧：(1) 
；（2） 
； （3）
；（4）
；此外，需注意裂项之后相消的过程中容易出现丢项或多项的问题，导致计算结果错误.
科目：高中数学 来源： 题型：
【题目】某科研机构研发了某种高新科技产品，现已进入实验阶段.已知实验的启动资金为10万元，从实验的第一天起连续实验，第
天的实验需投入实验费用为
元
，实验30天共投入实验费用17700元.
（1）求
的值及平均每天耗资最少时实验的天数；
（2）现有某知名企业对该项实验进行赞助，实验
天共赞助
元
.为了保证产品质量，至少需进行50天实验，若要求在平均每天实际耗资最小时结束实验，求
的取值范围.（实际耗资=启动资金+试验费用-赞助费）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在直三棱柱ABC﹣A1B1C1中，AA1=AC=2AB=2，且BC1⊥A1C．
（1）求证：平面ABC1⊥平面A1ACC1；
（2）设D是线段BB1的中点，求三棱锥D﹣ABC1的体积．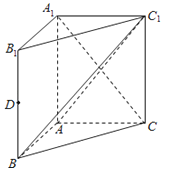
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x），当x，y∈R时，恒有f（x+y）=f（x）+f（y）．当x＞0时，f（x）＞0
（1）求证：f（x）是奇函数；
（2）若
， 试求f（x）在区间[﹣2，6]上的最值；
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系
中，曲线
的参数方程为
（
， 
为参数），在以
为极点， 
轴的正半轴为极轴的极坐标系中，曲线
是圆心在极轴上，且经过极点的圆.已知曲线
上的点
对应的参数
，射线
与曲线
交于点
.
（Ⅰ）求曲线
的直角坐标方程；
（Ⅱ）若点
， 
在曲线
上，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校从高一年级学生中随机抽取40名中学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成六段： 
， 
，…， 
，得到如图所示的频率分布直方图.
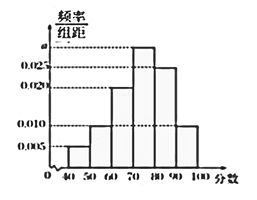
（1）求图中实数
的值；
（2）若该校高一年级共有640人，试估计该校高一年级期中考试数学成绩不低于60分的人数；
（3）若从数学成绩在
与
两个分数段内的学生中随机选取2名学生，求这2名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4－4：坐标系与参数方程
在直角坐标系
中，直线
的参数方程为
（
为参数），以原点
为极点， 
轴的非负半轴为极轴建立极坐标系，曲线
的极坐标方程为
（Ⅰ）求曲线
的直角坐标方程，并指出其表示何种曲线；
（Ⅱ）设直线
与曲线
交于
两点，若点
的直角坐标为
，
试求当
时， 
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
