
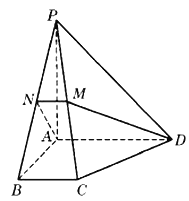
【题目】如图,在四棱锥![]() 中,底面为直角梯形,
中,底面为直角梯形, ![]() ,
, ![]() ,
, ![]() 垂直于底面
垂直于底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求四棱锥的体积![]() 和截面
和截面![]() 的面积.
的面积.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先根据线面垂直性质定理得![]() ,而
,而![]() ,所以由线面垂直判定定理得
,所以由线面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]() , 再由等腰三角形性质得
, 再由等腰三角形性质得![]() ,因此由线面垂直判定定理得
,因此由线面垂直判定定理得![]() 平面
平面![]() ,即证得
,即证得![]() ;(2)易得四棱锥
;(2)易得四棱锥![]() 的高
的高![]() ,再根据锥体体积公式得四棱锥的体积
,再根据锥体体积公式得四棱锥的体积![]() ;要求截面
;要求截面![]() 的面积,先确定截面
的面积,先确定截面![]() 的形状:由三角形中位线性质得
的形状:由三角形中位线性质得![]() ,即得
,即得![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() ,即四边形
,即四边形![]() 是直角梯形,最后利用直角梯形面积公式求解面积.
是直角梯形,最后利用直角梯形面积公式求解面积.
试题解析:(Ⅰ)证明:∵![]() 是
是![]() 的中点,
的中点, ![]() ,∴
,∴![]() ,
,
由![]() 底面
底面![]() ,得
,得![]() ,
,
又![]() ,即
,即![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() ,∴
,∴![]() 平面
平面![]()
∴![]() .
.
(Ⅱ)解:由![]() ,得底面直角梯形
,得底面直角梯形![]() 的面积
的面积![]() ,
,
由![]() 底面
底面![]() ,得四棱锥
,得四棱锥![]() 的高
的高![]() ,
,
所以四棱锥![]() 的体积
的体积![]() .
.
由![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,得
的中点,得![]() ,且
,且![]() ,
,
又![]() ,故
,故![]() ,由(Ⅰ)得
,由(Ⅰ)得![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
故![]() ,∴四边形
,∴四边形![]() 是直角梯形,
是直角梯形,
在![]() 中,
中, ![]() ,
, ![]() ,
,
∴截面![]() 的面积
的面积![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①三点确定一个平面;
②三条两两相交的直线确定一个平面;
③在空间上,与不共面四点A,B,C,D距离相等的平面恰有7个;
④两个相交平面把空间分成四个区域.
其中真命题的序号是 (写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B是海面上位于东西方向相距5(3+![]() )海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20![]() 海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?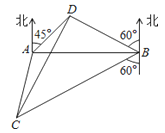
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域D,如果存在正实数m,使得对任意x∈D,都有f(x+m)>f(x),则称f(x)为D上的“m型增函数”.已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=|x﹣a|﹣a(a∈R).若f(x)为R上的“20型增函数”,则实数a的取值范围是( )
A.a>0
B.a<5
C.a<10
D.a<20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强市民的环保意识,某市面向全市增招环保知识义务宣传志愿者,从符合条件的志愿者中随机选取![]() 名志愿者,其年龄频率分布直方图如图所示,其中年龄(岁)分成五组:第
名志愿者,其年龄频率分布直方图如图所示,其中年龄(岁)分成五组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图(局部)如图所示.
,得到的频率分布直方图(局部)如图所示.
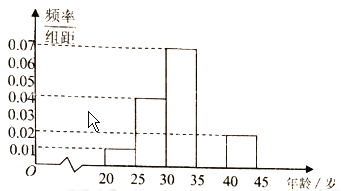
(1)求第![]() 组的频率,并在图中补画直方图;
组的频率,并在图中补画直方图;
(2)从![]() 名志愿者中再选出年龄低于
名志愿者中再选出年龄低于![]() 岁的志愿者
岁的志愿者![]() 名担任主要宣讲人,求这
名担任主要宣讲人,求这![]() 名主要宣讲人的年龄在不同一组的概率.
名主要宣讲人的年龄在不同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=bax , (其中a,b为常数且a>0,a≠1)的图象经过点A(1,8),B(3,32)
(1)求f(x)的解析式;
(2)若不等式![]() +1﹣2m≥0在x∈(﹣∞,1]上恒成立,求实数m的取值范围.
+1﹣2m≥0在x∈(﹣∞,1]上恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二次函数f(x)=ax2+bx+c的图象过点(0,1)和(1,4),且对于任意的实数x,不等式f(x)≥4x恒成立.
(1)求函数f(x)的表达式;
(2)设g(x)=kx+1,若F(x)=g(x)﹣f(x),求F(x)在[1,2]上的最小值;
(3)设g(x)=kx+1,若G(x)=![]() 在区间[1,2]上是增函数,求实数k的取值范围.
在区间[1,2]上是增函数,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,⊙O与⊙O′相交于A、B两点,过A引直线CD,EF分别交两圆于点C、D、E、F,EC与DF的延长线相交于点P,求证:∠P+∠CBD=180°.
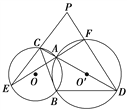
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com